Overview and Objective
This activity aims to enhance students’ creative thinking in mathematics. Students will learn about tangram paradoxes and solve the illusions using the area conservation principle.
Warm-Up
According to an ancient Chinese legend, an old wise man was tasked with constructing a window at the Chinese emperor's palace. He wrapped a square glass in the silk, but upon arriving at the palace he dropped the pane, and the square glass had broken into seven geometric pieces. He attempted to collect the pieces back, but he came up with a different shape every time he tried. In the end, the emperor became more pleased with the infinite amount of combinations and interesting shapes.

Soon the puzzle was reincarnated with paper, wood, and other materials and spread across the world. When re-creating a tangram puzzle, one must construct the pieces carefully by measuring and calculating the angles, sides, and area measures.
If students are not familiar with Tangrams on Mathigon, you may introduce them using the Mathigon Tangram Activity and allow them to work on any of the puzzles for 5 minutes or so. As they are exploring the puzzles, ask them to note any strategies that are working well for them as well as any puzzles they are having difficulty solving. After 5 minutes or so, invite students to share some observations with the class.
Main Activity
One of the interesting things about tangram puzzles is tangram paradoxes. A paradox is a statement that seems to contradict itself because it combines words or ideas that cannot be true at the same time. In some cases, we think of paradoxes as riddles or questions of logic. Tangram paradoxes are designs that can be made with all seven pieces and appear to be identical in appearance yet have slightly different configurations.
You may use the Polypad here to demonstrate a paradoxical tangram example;
Use all seven tangram pieces to create these designs;
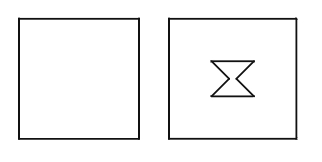
We already know that seven tangram pieces can be assembled as a square.
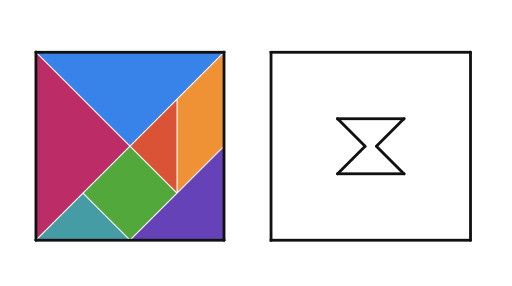
You may invite students to create the design at the left using the same seven tangram pieces.
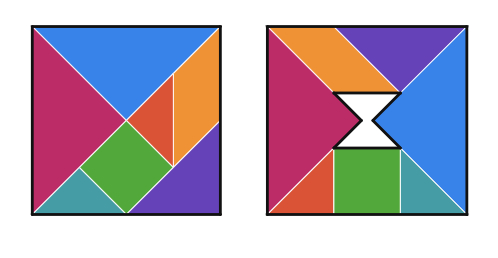
Now they have seen that using the same seven pieces, one can create two seemingly identical squares but one with a hole! Here, It seems like a magical piece vanishes on the right square.
Ask students how can they explain this paradox. Share the Tangram Paradoxes Student Version Polypad with students to further investigate the square designs. Invite them to share their ideas.
Discuss that the total surface area of the pieces never changes. To understand the illusion, we need to check the side lengths of the designs carefully. Students may use the grid backgrounds or the ruler to prove their ideas.
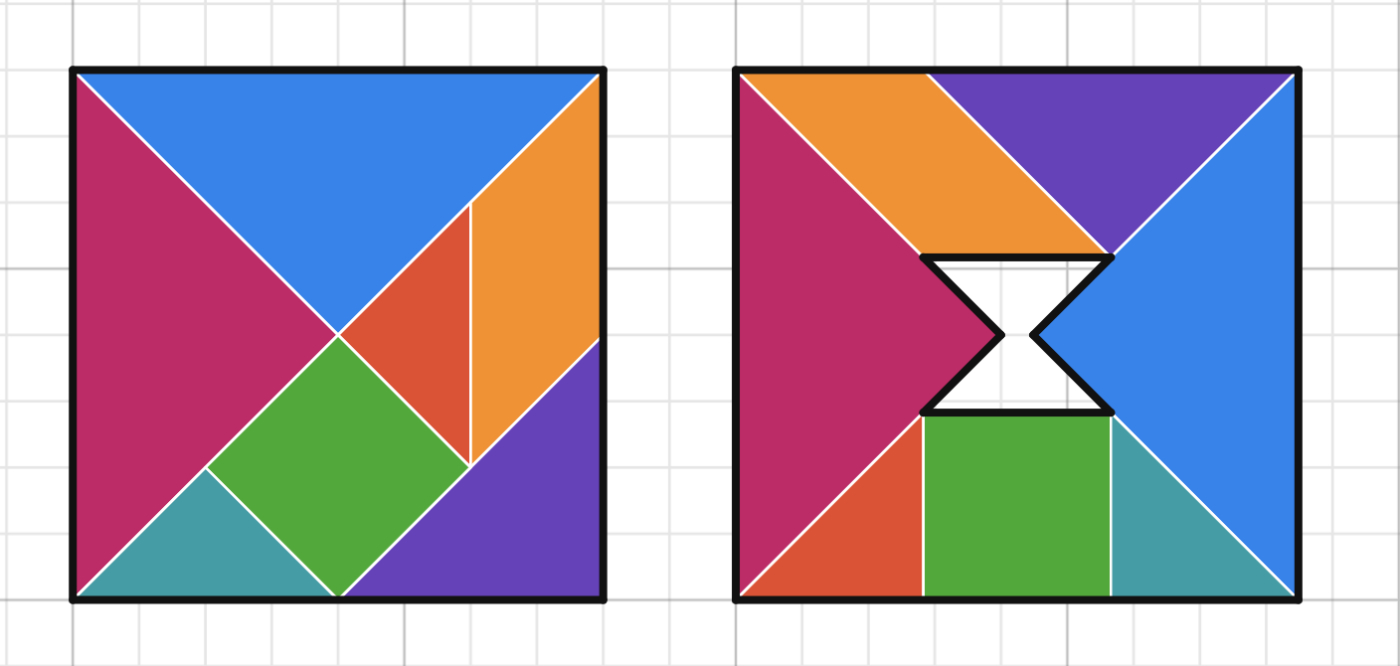
Both shapes have the same height but the right shape is not a square (as the left one is), but a rectangle.
There are many similar paradoxes by which tangram puzzles can be assembled, but when you check the side lengths, you will see that shapes differ a little in size. Let students work in pairs to complete all the tangram paradoxes.
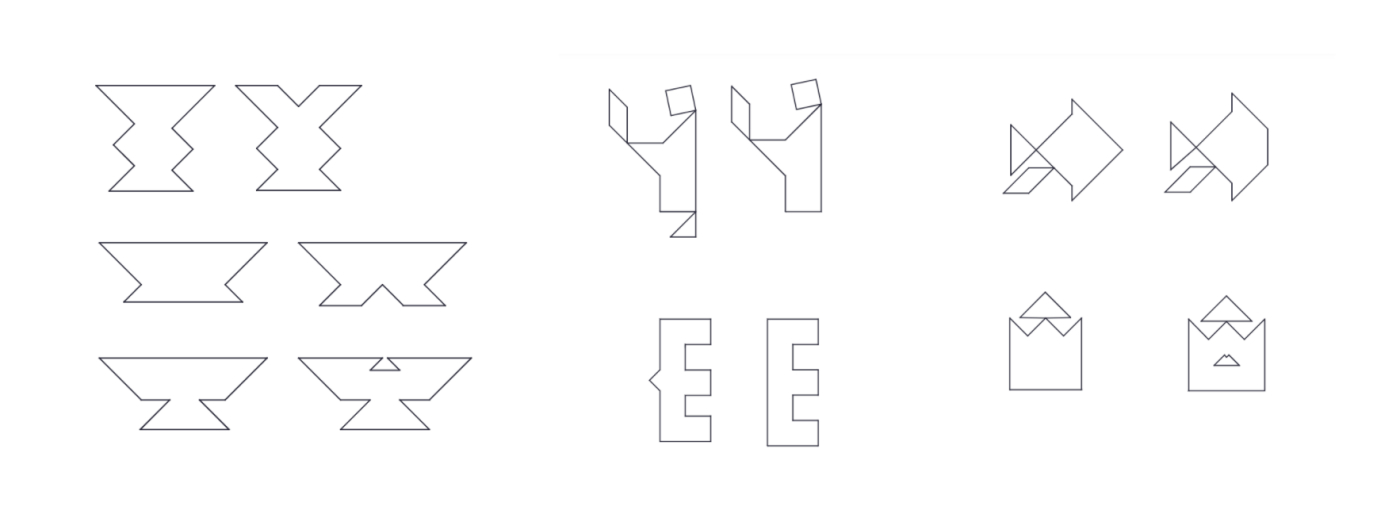
Closure
Share some student work with the class. Discuss with students that the solutions look the same visually, by measuring them one will realize that one of the figures is slightly larger than the other one. To close the lesson, ask students to create their paradoxical tangram designs.
Support and Extension
For students ready for additional extension in this lesson, consider sharing the Magic Egg Tangram task. For younger grades, you may show the heart tangram and ask them to re-create the tangram pieces using the Polypad tools.