Shapes Around a Vertex

Lesson outline

Polypad includes eight regular polygons. This task encourages students to explore the angles in each polygon and discover which can be joined together to fit around a point with no gaps. It could lead to work on tiling and tessellations as well as developing students’ capacity to work systematically and reason clearly. Depending on prior attainment and the length of the lesson, it may be necessary to split this activity over two lessons, with the first focussing on finding the interior angles of regular polygons and the second focussing on finding combinations of polygons that meet around a vertex without leaving gaps.

Lesson objective: Solve problems involving interior angles in regular polygons

Lesson activity

Warm-up

Begin the lesson by discussing how to work out the interior angles in a regular polygon. You could start by drawing a table and asking students to fill in any that they already know, or give them a partially filled table and challenge them to fill in the rest.

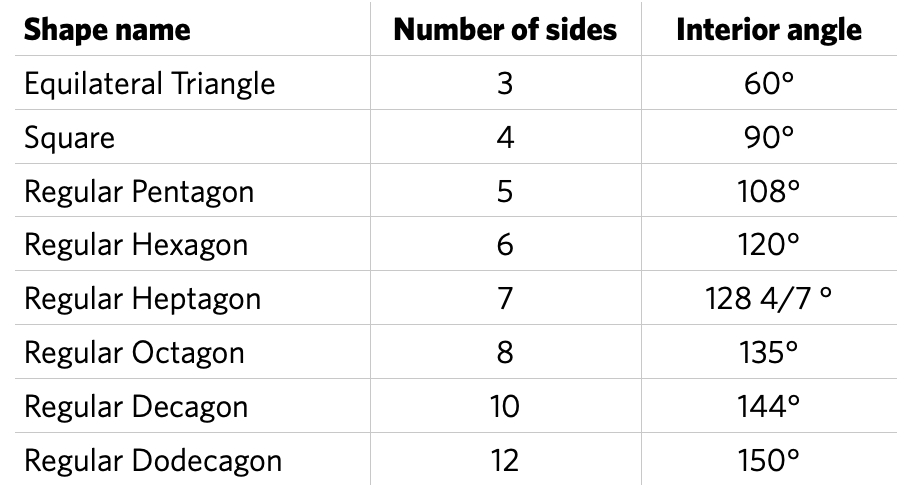
Students could use the polygons in Polypad and the pen tool to show how they have calculated the interior angle. Here are three examples, using a regular decagon, to show methods they might use or that you might choose to share with them:

1. Divide the decagon into 10 equal isosceles triangles by joining each vertex to the centre. The centre angle is 360° ÷ 10 = 36° so the other two angles must be 72°. Therefore, each interior angle is 72° + 72° = 144°.
2. The decagon can be divided into eight triangles by joining from one vertex to every other non-adjacent vertex. Therefore, the sum of the interior angles is 8 µ 180° = 1440°, so each interior angle is 144°. (This method does not rely on the decagon being regular and can be adapted to find a formula for the sum of the interior angles of any polygon.)
3. Adding up all the exterior angles creates one full turn (360°), so the size of each of the ten exterior angles has to be 360° ÷ 10 = 36°. This means that the supplementary interior angles is 180° – 36° = 144°.

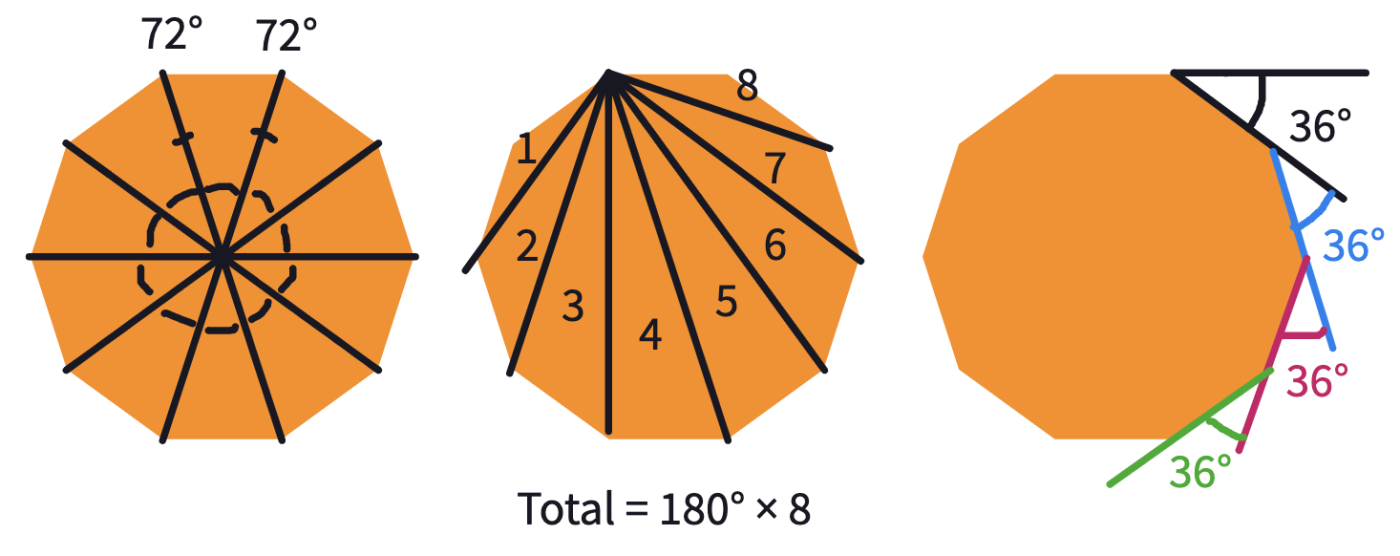
Students could also use the protractor tool in to measure each angle.

Main Activity

Show students these the two arrangements of shapes. Ask students whether the shapes fit exactly together in either arrangement. Expect some disagreement; from the image it looks like there is a small gap on the right hand image, but some students may not be convinced that the left hand image is an exact fit either.

Challenge students to come up with a mathematical way, using their knowledge of interior angles, to convince you whether the shapes fit exactly or not. They could annotate the arrangements using the pen tool in Polypad, or work on paper to show the calculations necessary.

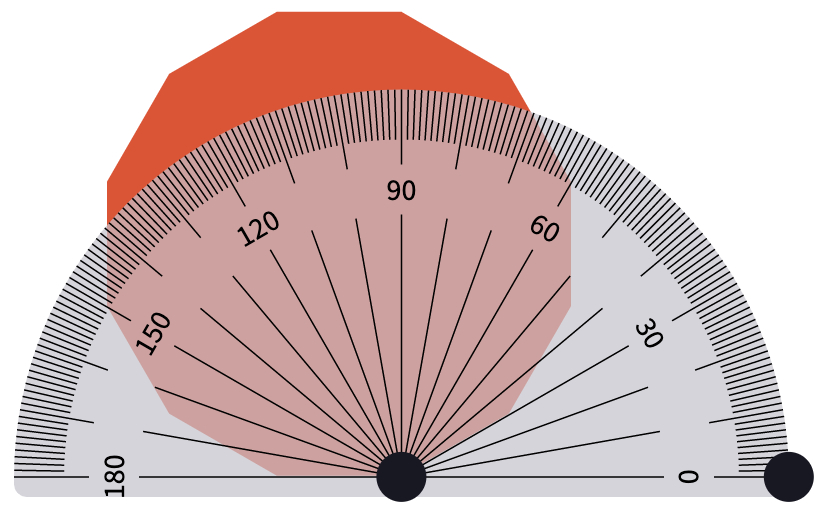
The left image consists of a dodecagon (150°), a hexagon (120°) and a square (90°) so the angle sum at the vertex where they meet is exactly 360°. The right image has a heptagon (128 4/7°), a pentagon (108°) and a hexagon (120°), so the angle sum is 356 4/7°, close to but not exactly 360°.

If students are struggling, they can also use Mathigon’s protractor tool to manually measure the internal angles of a polygon.

Bring the class together to share their reasoned arguments, and then set the next challenge: Can you find all the ways that these eight regular polygons can fit together around a point without leaving a gap?

Here is a canvas with the eight regular polygons. You may need to remind students that they should only use these eight shapes and not any of the others offered in the toolbar. Students could start by just trying out different combinations of shapes in Polypad that look as if they might fit without gaps.

Encourage them to calculate with angles to show that the total is 360°, and suggest that they could work out a combination of angles first and then use Polypad to demonstrate that the shapes do indeed fit together. Younger students might want to annotate their diagrams to show this calculations and the angles meeting at every vertex.

Towards the end of the lesson, bring the class together to share findings. You could collect on the board examples that they have found, and invite students to explain how they found particular combinations that worked. A nice way to round off the lesson is to show students that many of the combinations they have found can be extended into tessellation patterns that cover the plane.

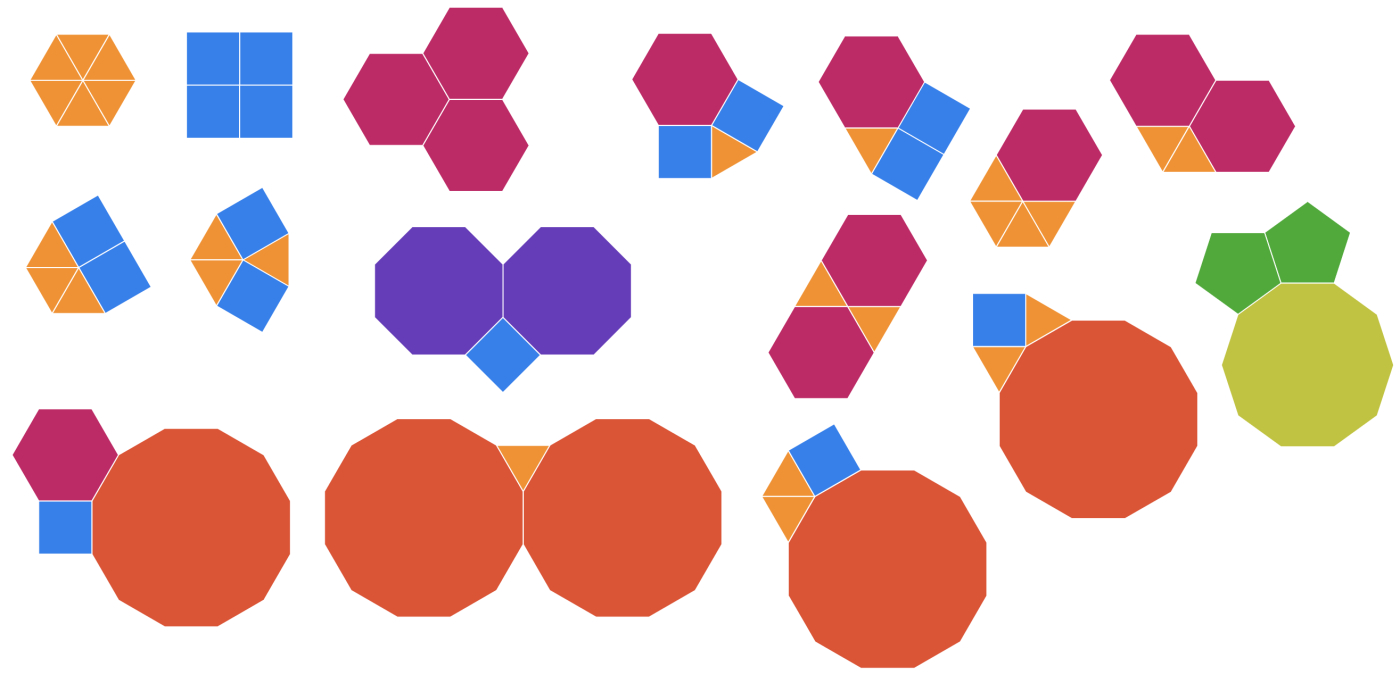
Possible solutions

Below are all possible solutions. If students are struggling, you could give them a few of these examples, and a few incorrect examples that are close but not quite 360°. Then ask students to work out the angles in each case and sort them correctly.

Support and extension

For a simpler challenge, invite students to make as many combinations that add to 360° as they can using the equilateral triangle, square, and hexagon. Another possible challenge could be to find as many ways as they can to make a hexagon using these four shapes:

Students could also try to write a convincing explanation why the 16 arrangements above are indeed all the possible choices.

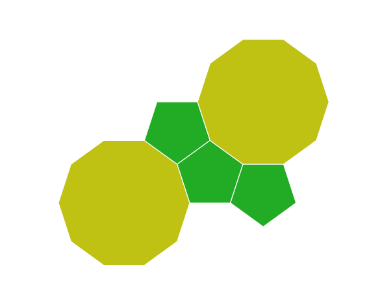
As an extension, students could consider which of the arrangements above could be extended to form tessellations and why others can’t. For example, in this arrangement, for a tessellation to continue, the pentagon in the center would need to have an alternating pattern of decagons and pentagons around it, but as it has an odd number of sides, the pattern breaks down.

Tessellations could then be explored further in a later lesson.