Computer based images are made up of thousands of tiny dots of color called pixels. They are the smallest unit in a digital display.
A pixel is represented by a dot or square on a computer monitor display screen.
To draw a line on the computer screen, you simply need to color the squares that depict the line.
Invite student use this polypad to create vertical, horizontal and tilted lines by coloring the pixels. Use notice and wonder routine to compare the number of colored pixels and the length of each line.

How many pixels should we color in to depict a line?
Main Activity
Although the number of colored pixels to draw vertical or horizontal lines is very straightforward, the tilted lines like the diagonals of a rectangle worth exploring!
Diagonals are the line segments that connect two non-adjacent vertices of polygons. Rectangles have two diagonals that connect two opposite vertices. They are the same size.
The pink line segment here represents the tilted line we would like the draw using the pixels.
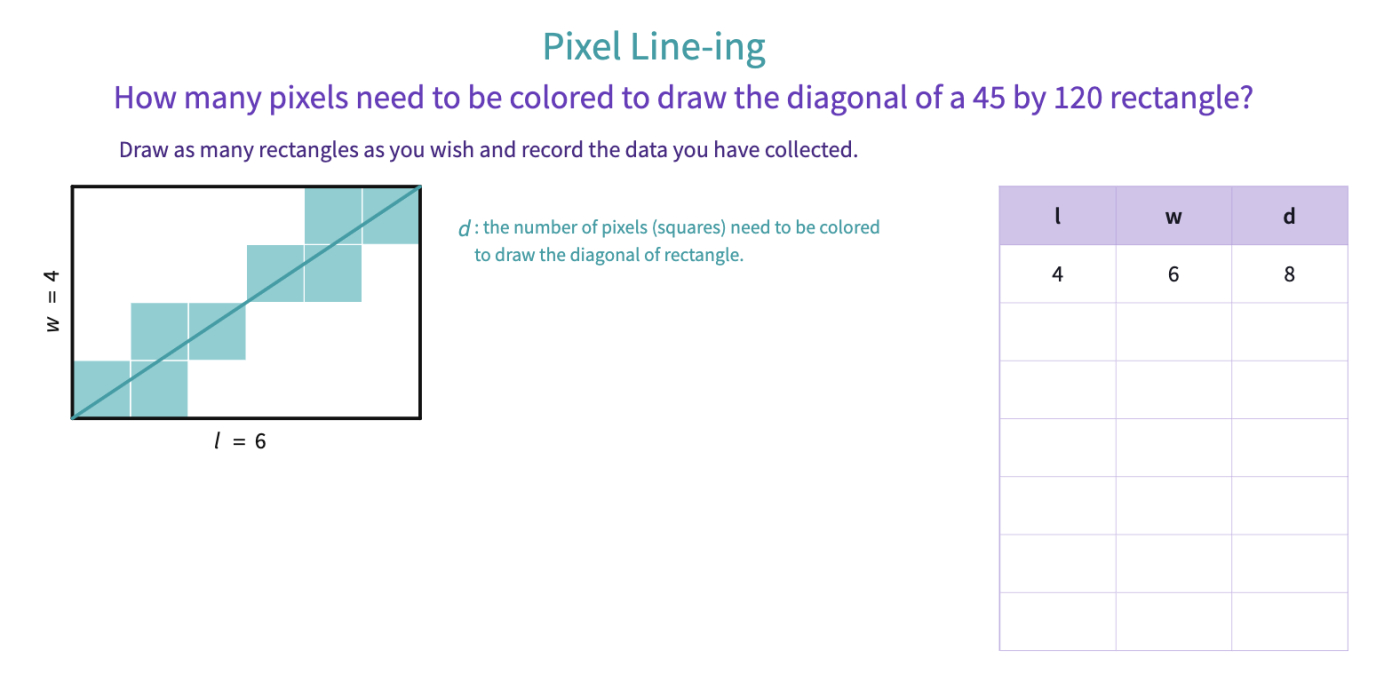
Invite students to count the number of squares the diagonal passes through.
Clarify that to draw the diagonal of a 6 x 10 rectangle, we color 14 pixels (squares).
Many things can vary in these rectangles: the width, the length, and the number of squares the diagonal passes through (or is "cut"). One of the strategies we can use is keeping one of these variables constant to find the pattern.
Click here to share the canvas with the students. To figure out the relation among , and , you may need to draw many examples. At the start, you may not be ready to answer the first question, but see if you can build up to that.
Display students screens to discuss about the visual patterns. Ask students if the visual patterns formed by the colored squares can help them to figure out the number patterns.
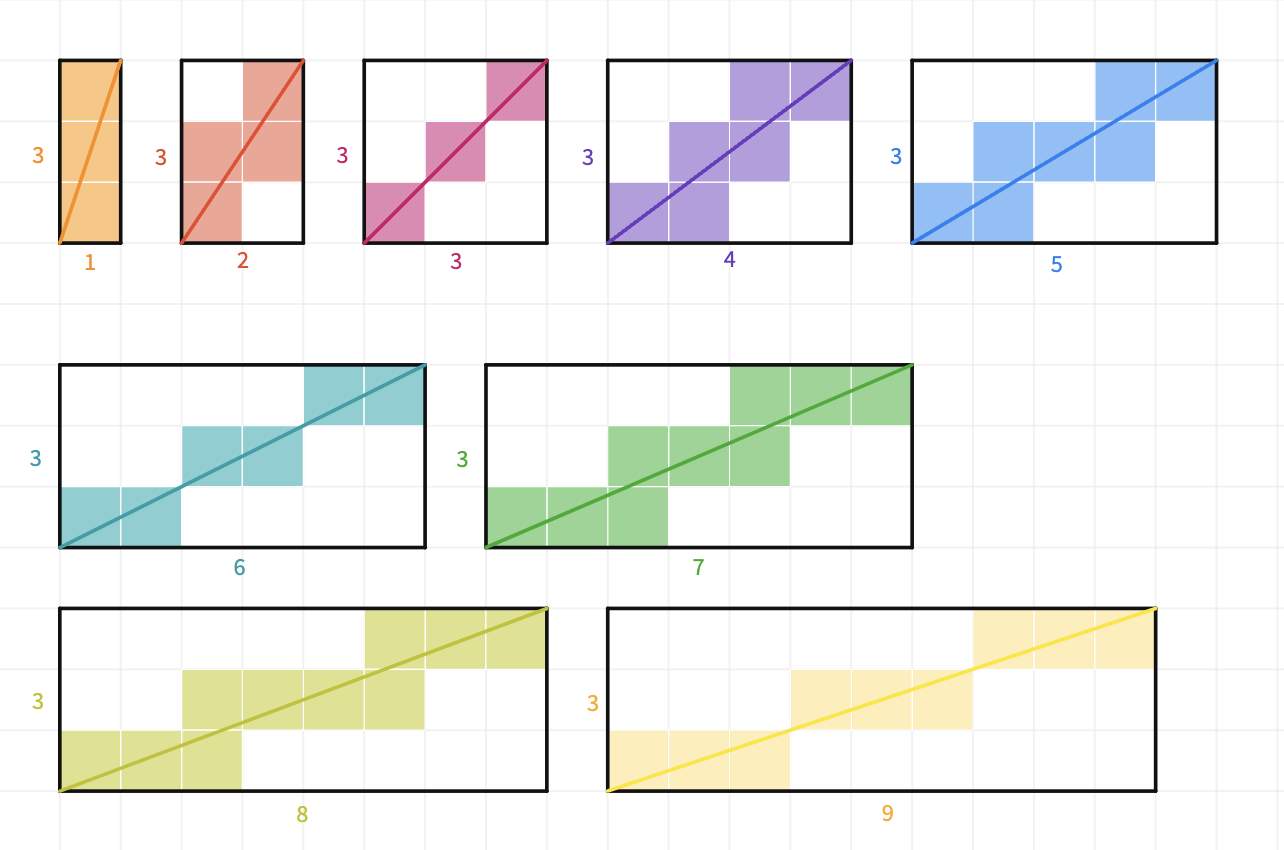
- If some students already figured out that the visual patterns are effected by the dimensions, ask them to lead a class discussion about the dimensions being multiple of each other, being prime or relatively prime ..
- if not, invite students to explore differences between how the squares are aligned when the length and width have common factors and when they don't.
- How will the pixel squares align in a square?
- How will the squares align when the length of the rectangle is a multiple of the width ?
Hint
Help students to conclude that the number of colored pixels to draw each diagonal is always less than the sum of length and width. But that difference changes depending the size of the rectangles.
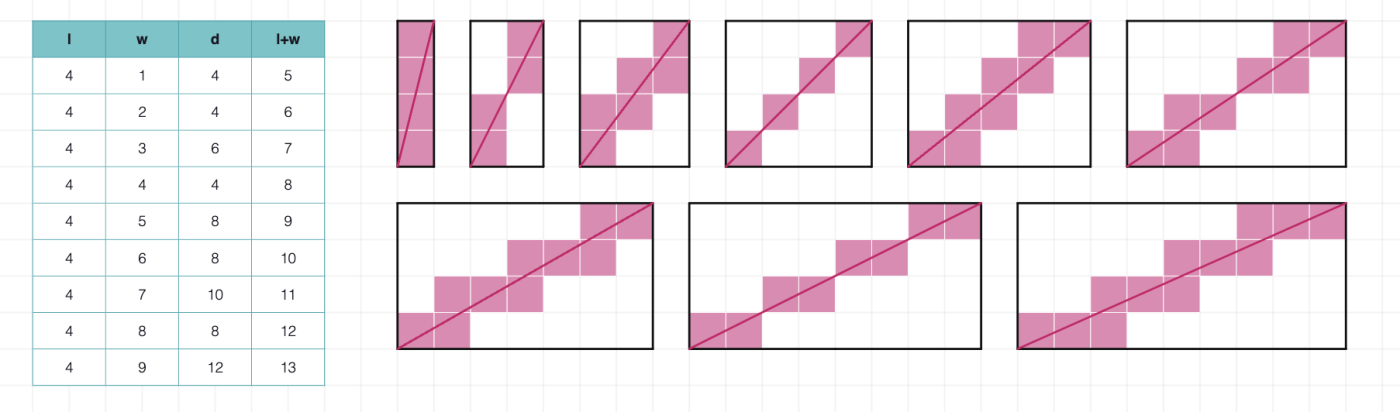
If students need extra guidance, invite them to explore rectangles such as , , , and .
After they made their drawings, use the notice and wonder routine. If it does not come up naturally ask students, if they notice a pattern in the differences betweenand d when the length and width have common factors.
Solution
The number of colored pixels () to draw the diagonal of a rectangle is
.
So to draw a tilted line which has the same length of a rectangle’s diagonal, we need to color pixels!