Overview and Objective
In this lesson, students will use two variables to represent numbers and write expressions for each term of the Fibonacci-like sequence. They will predict the next terms of the sequence and will make observations about the connections among different terms. Students will practice using distributive property to notice equivalent expressions.
Warm-Up
Here is a number sequence with five terms. Ask students if they can spot the rule?

Invite them to share their thinking and ask them to find the next few numbers in the sequence. Clarify with students that the third number is the sum of the first two numbers and the fourth number is the sum of the second and third number, and so on...
Main Activity
Share this canvas with students and ask them to complete given number sequences by choosing a different second number each time. Clarify that each new term should be found by adding the two numbers before it.

Let students share their sequences. Copy and record some of them on a teacher's canvas where students can see all the sequences together. Ask them what they notice and wonder. Here are some possible sequences;

Ask students if they can predict the fifth, sixth, or tenth number when the second number is 150.
You may remind them to use a systematic approach to help them get into the problem. For example, looking at the sequence of cells that begin, 1-1, 1-2, 1-3, 1-4,... will make it easier for them to predict the following numbers in the sequence.
They might come up with the observations such as;
- the fourth number is twice the second the number plus one.
- In this case, you may ask them to change the first number and make another observation regarding the fourth number.
- The fifth number is twice the second the number plus two.
- Again, you may ask them to change the first number to repeat their observations.
- The sum of the first and fifth numbers is three times the sum of the first two.
- Here, you may ask them to express their observations algebraically.
If students need guidance, you may ask them to use and for the first and second numbers and write the rest of the sequence algebraically.

If students are familiar with the Fibonacci Sequence, they will notice that the coefficients of and are the Fibonacci sequence numbers.
You may ask older students to express any number in the sequence in terms of the first and second numbers.
Closure
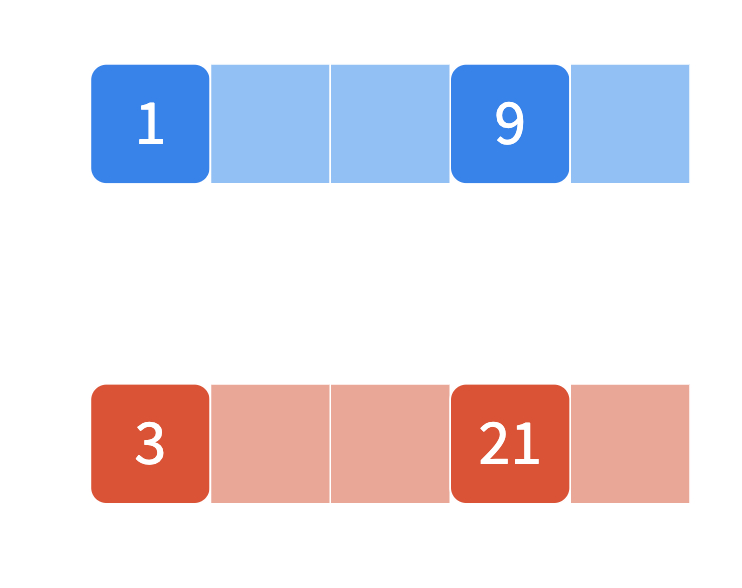
To close the lesson, ask students to fill in the missing numbers in this sequence using the same rule by sharing this canvas.
Also, let them create sequences where they pick the first and fourth numbers. Again, if you are using this activity with older students, you may also ask them to re-write the algebraic expressions for each cell.

Extension
For students ready for additional extension in this lesson, consider creating a sequence where the third number is the arithmetic average (mean) of the first two.
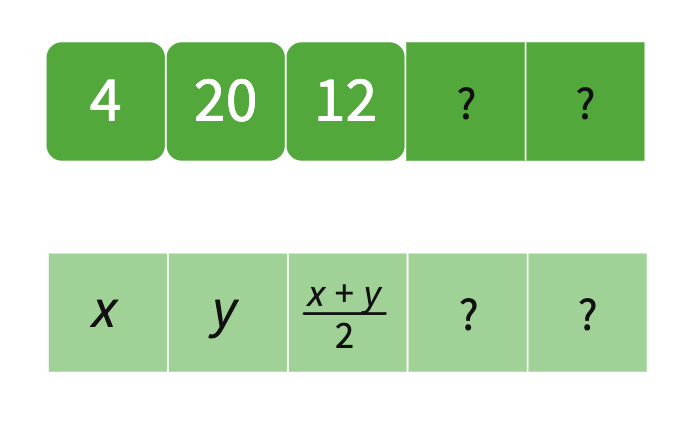
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.