Overview and Objective
In this lesson, students learn about one of the oldest mathematical stories while exploring the volume of a cube, constructible numbers, square root, and cube root numbers.
Warm-Up
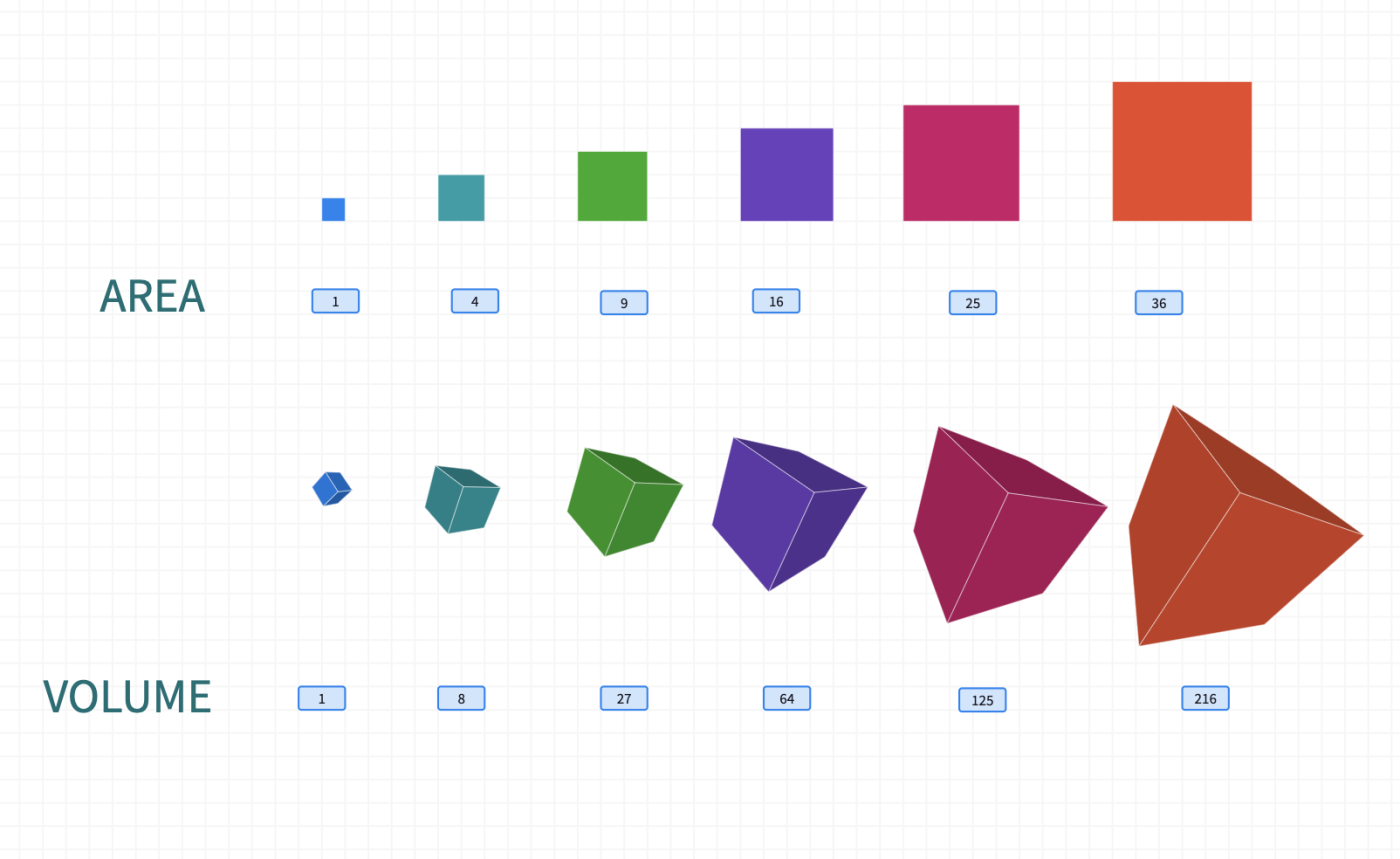
Share this polypad with students and invite them to work on the area of the squares and volume of the cubes. Click here to learn how to share polypads with students and how to view their work. After a few minutes of work time, share some student work with the class. Share the numbers like 1, 4, 9, 16 .. are called square numbers, whereas 1, 8, 27, 64... are cube numbers. Discuss which numbers are both square and cube numbers.
Main Activity
Share the following legend with students:
According to legend, the city of Delos in ancient Greece was once faced with a terrible plague. An oracle told them that this was a punishment from the Gods, and the plague would go away if they built a new temple that was exactly twice the volume of the existing one. Delians doubled the edges of the temple, but the plague did not stop. What went wrong?
Share this canvas with students and give them some time to let them work on the problem. Students should use the custom polygon to create a cube with the given conditions.

Students are challenged to create additional cubes with twice the area and the volume, as well as the one that Delians built. Students may discover that when Delians doubled the edges, the new temple had an area 4 times bigger and a volume 8 times bigger. Since they were tasked with doubling the volume, they did not stop the plague. Ask them how to fix that historical mistake.
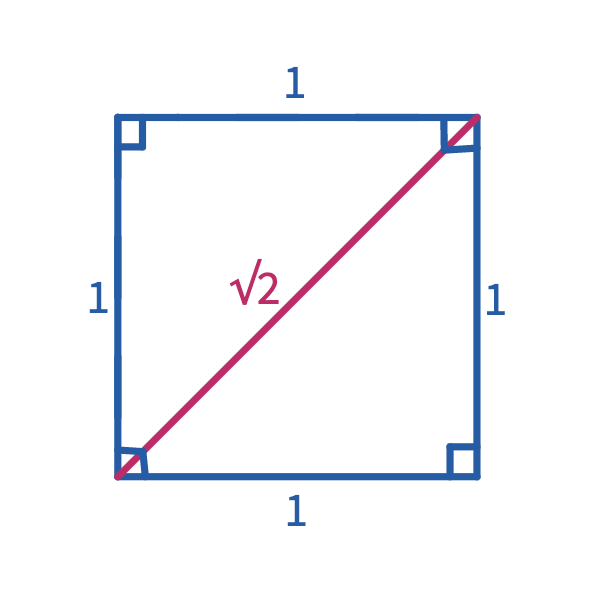
Let's first try doubling the area. Use the pink free polygon to create the new cubic temple with twice the area.After students figure out the side length must be , ask them to create a square with this side length. Some of the students may remember is the diagonal length of a 1 x 1 square. They can use this idea to create the square, then the net of the cube.
Explain that the tools that Delians use at the time are only a compass and straightedge. However, they could still construct a length of to double the area of the cube.
The √2 is the length of the hypotenuse of a right triangle with legs of length 1. Therefore it can be constructed using a compass and straightedge, which makes √2 a constructible number.
Now, it is time to create a cube with twice the volume. In algebraic terms, doubling a unit cube requires the construction of a line segment of length , where = 2
in other words, x = , the cube root of two.
After students figure out the side length, let them try to create a square with this side length using the pink free polygon tool on the canvas. They will realize that it is not as easy as constructing √2. In fact, it is not possible to construct this number using a compass and a straightedge. is not a constructible number
That's why doubling the volume of a cube, in fact, for that time was an impossible request.
Closure
You can close the lesson by mentioning that doubling the cube is one of the 3 main geometric problems in history (Geometric Problems of Antiquity) whose solutions were sought using only compass and straightedge:
- Circle Squaring
- Doubling a cube
- Trisecting an angle
More than 2000 years after they were formulated, only in modern times were all three ancient problems proved insoluble using only compass and straightedge. Today, there are ways to draw a line segment with a length of without the restriction of using a compass and a straightedge.
Support and Extension
For students ready for additional extension in this lesson, consider asking questions like constructing line segments with side lengths of √3, √5,√6.. and so on a blank Polypad canvas with a square grid background.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.