Introduction
I grew up in an old Victorian house in Adelaide, Australia, and every room in that house had a pressed-tin ceiling patterned with some design. The pattern on my bedroom ceiling was particularly straightforward, but it was inspirational!
He's me starting to tell the story about it.
I made up lots of puzzles based on staring at that grid of squares night after night. But here is the one puzzle that stuck with me ... for years!
The Puzzle
In the video, I showed a path that works starting from the top left corner of the grid. Can you find a path that starts from the top right corner and visits each and every cell in the grid exactly once, taking only vertical and horizontal steps? Try it! You can use any of the writing tools and also change the color as you wish!
There are actually lots of ways to complete this task. Was the way you found different from these two ways?
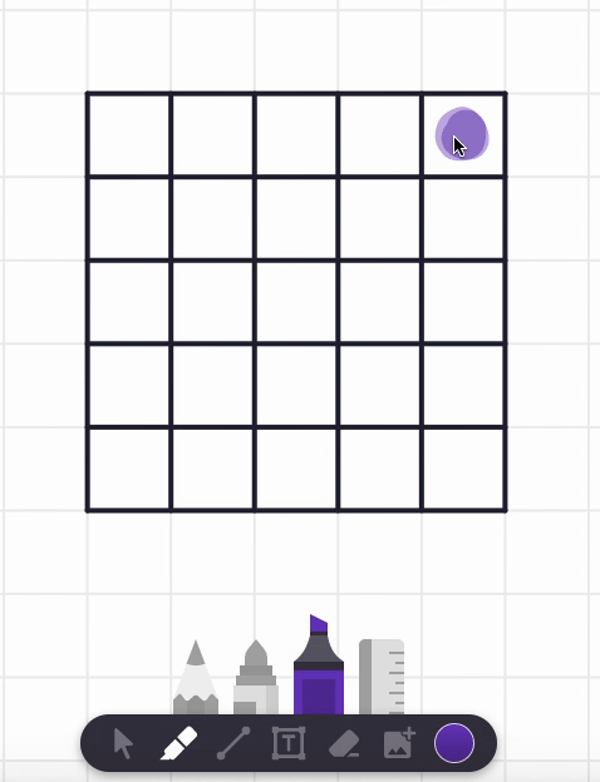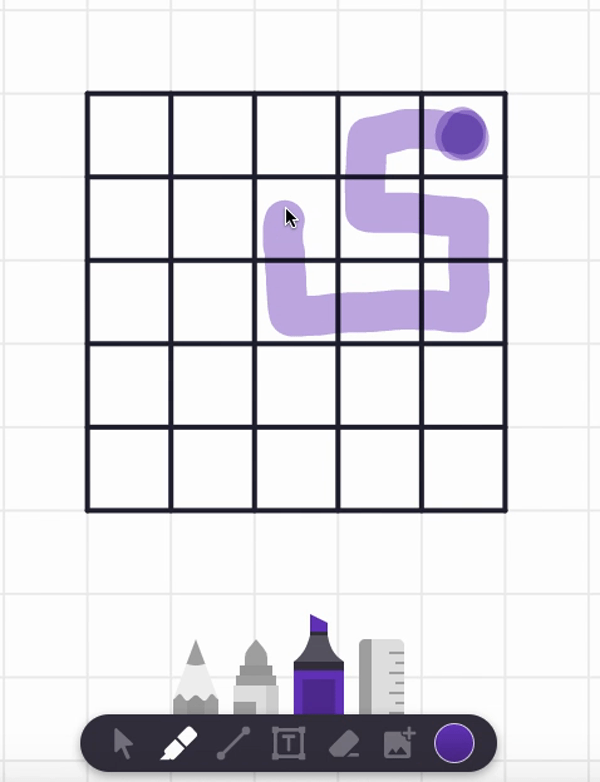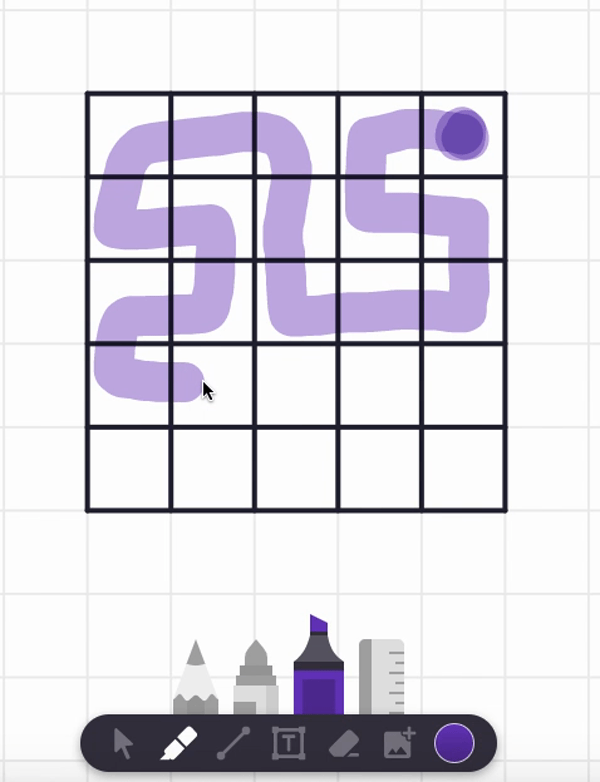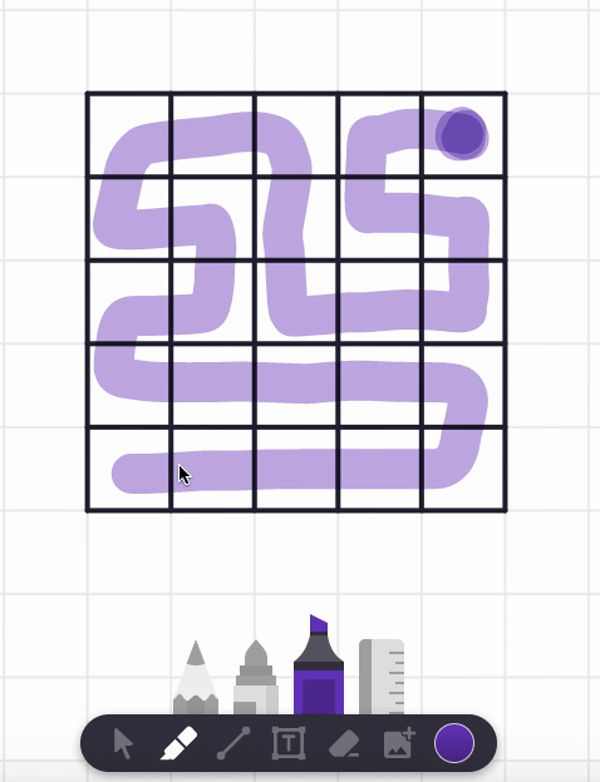
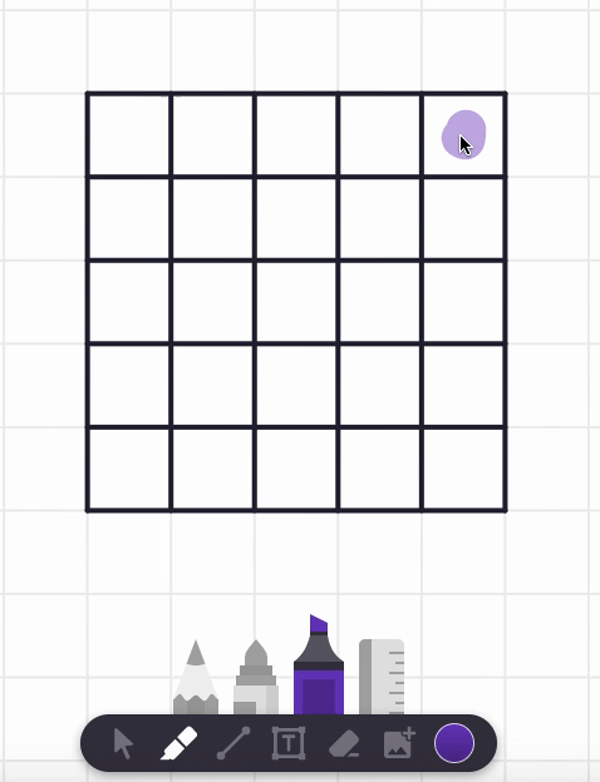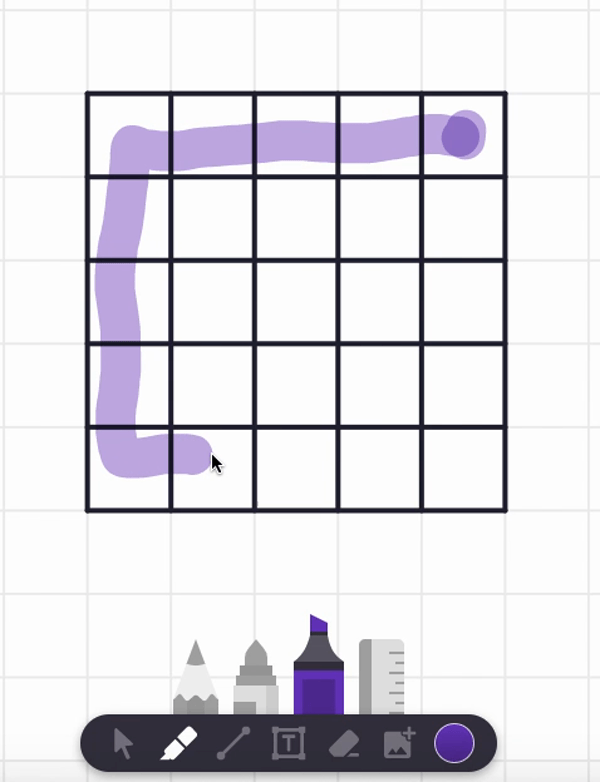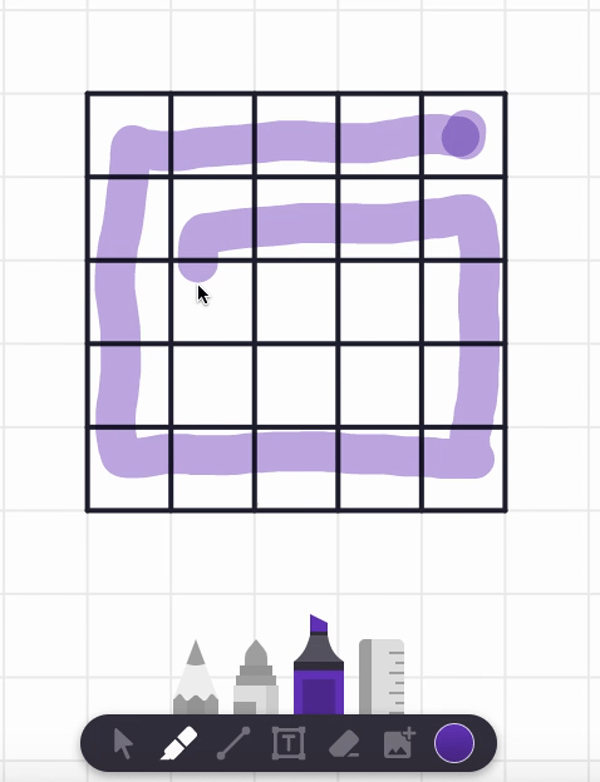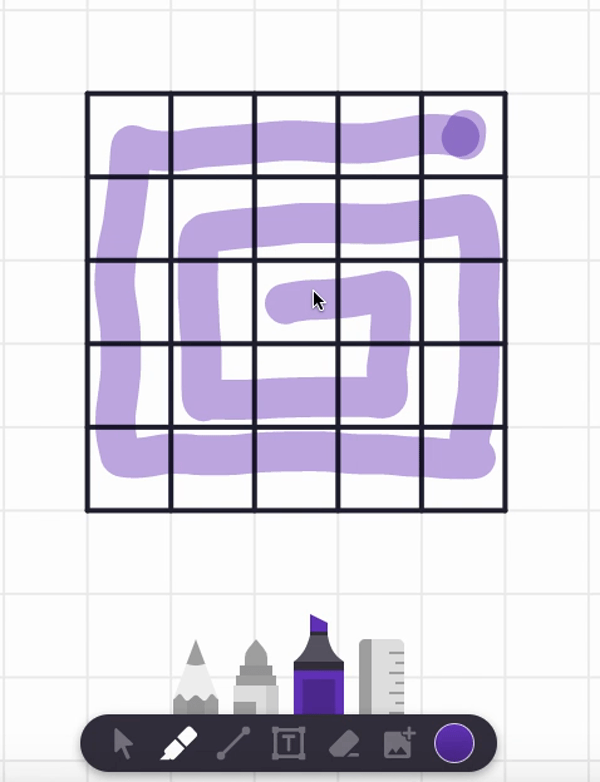
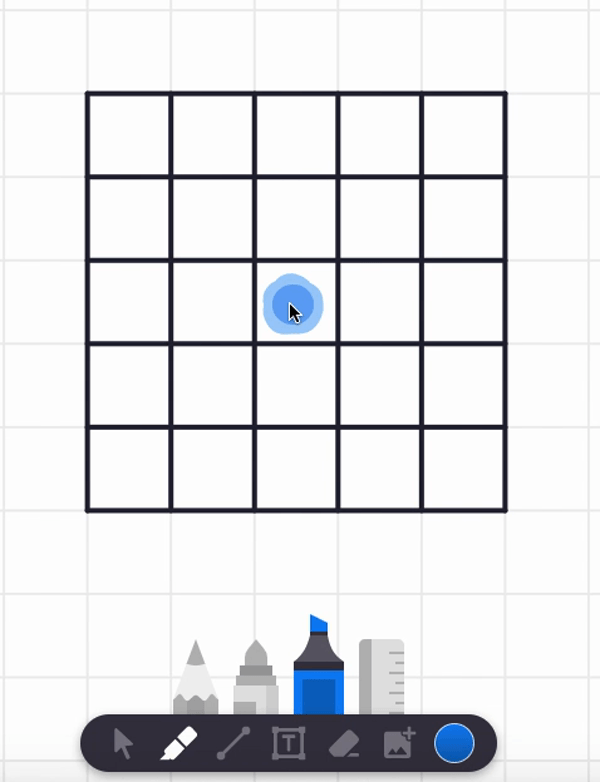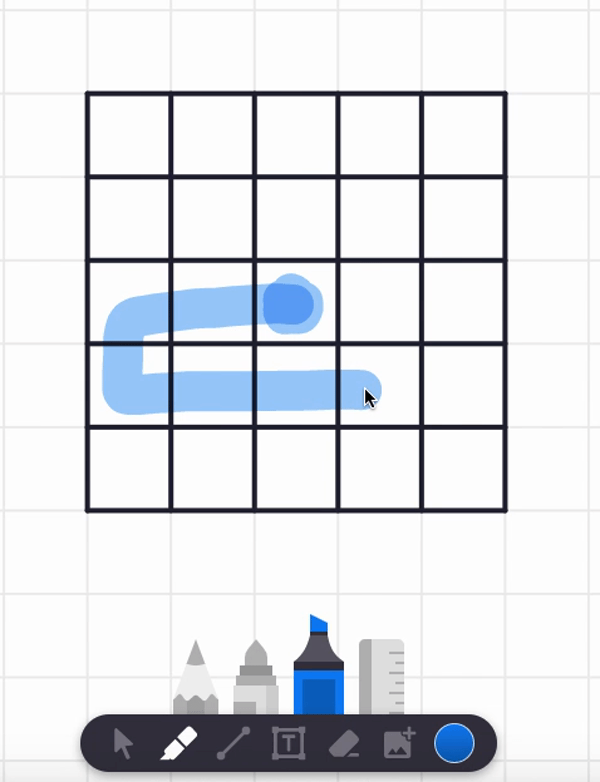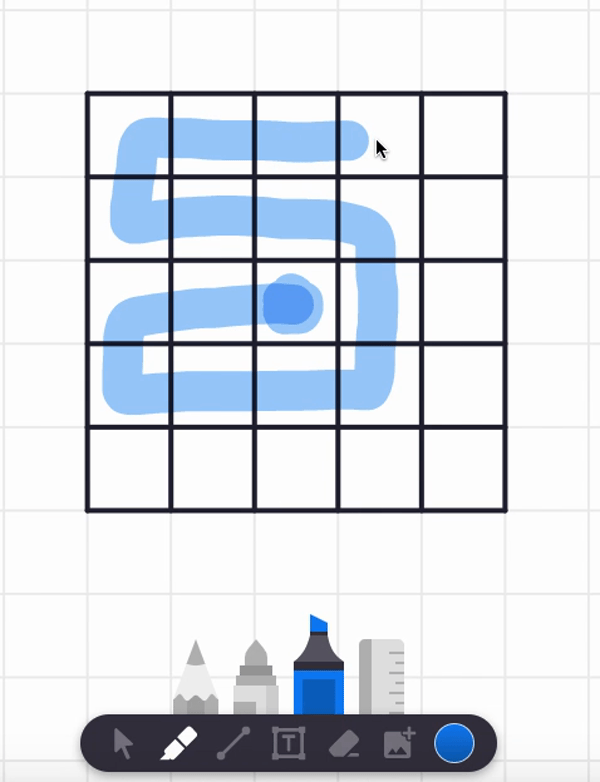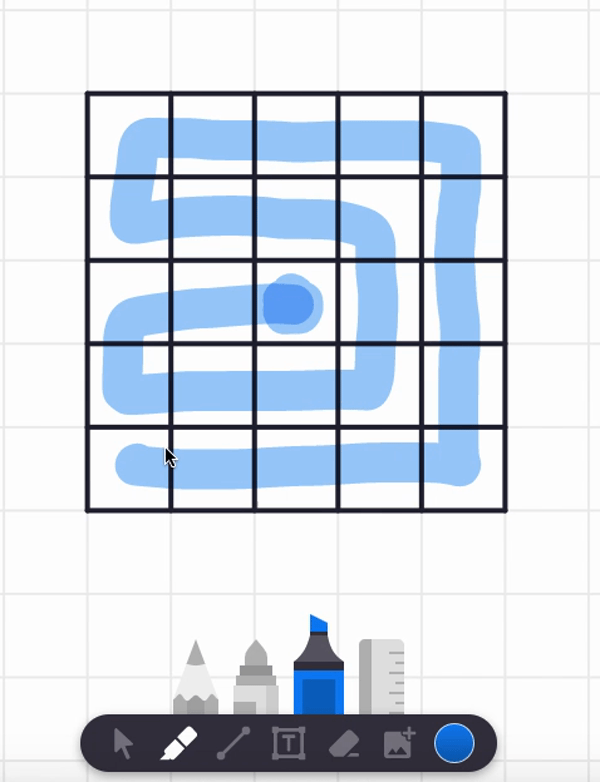
In the video, I also tried starting at the center square and found a spiral path that visits each and every cell. But are there any non-spiral paths that work too? Can you find such alternative answers?
Here are two different answers. Your answer might be different from these! It seems there are lots of paths that work from these starting point.
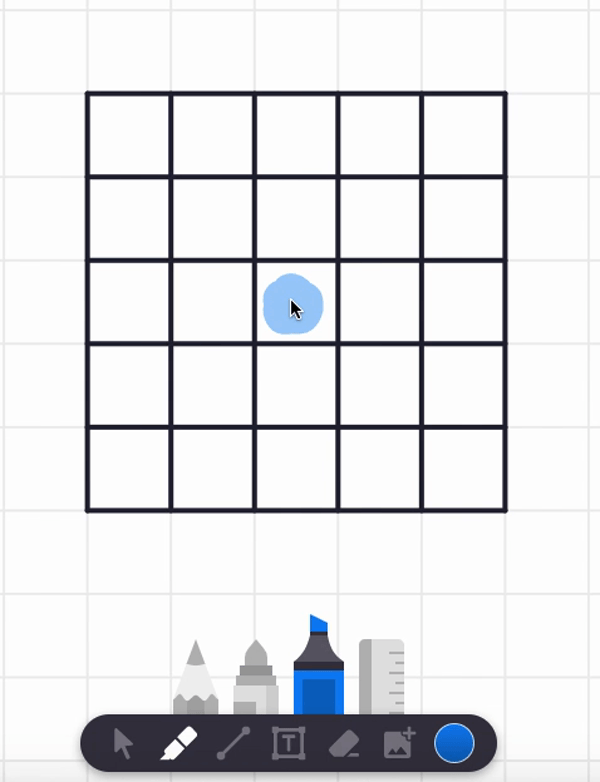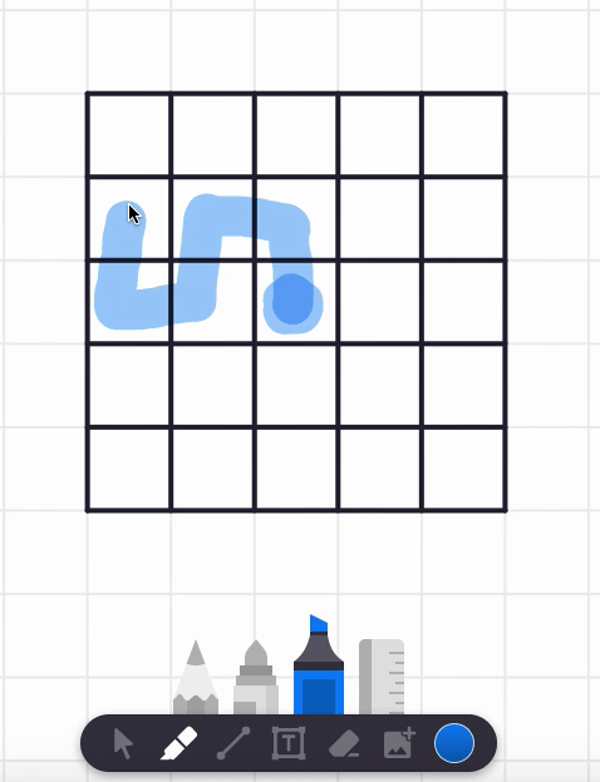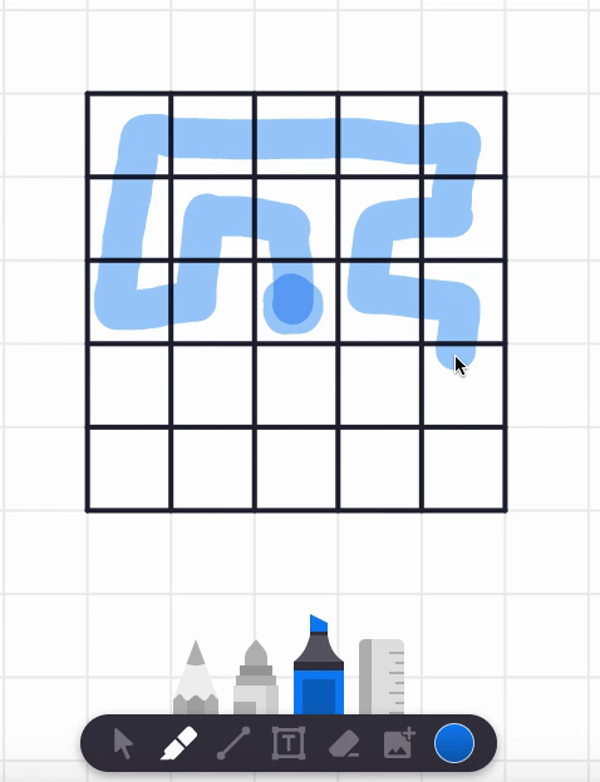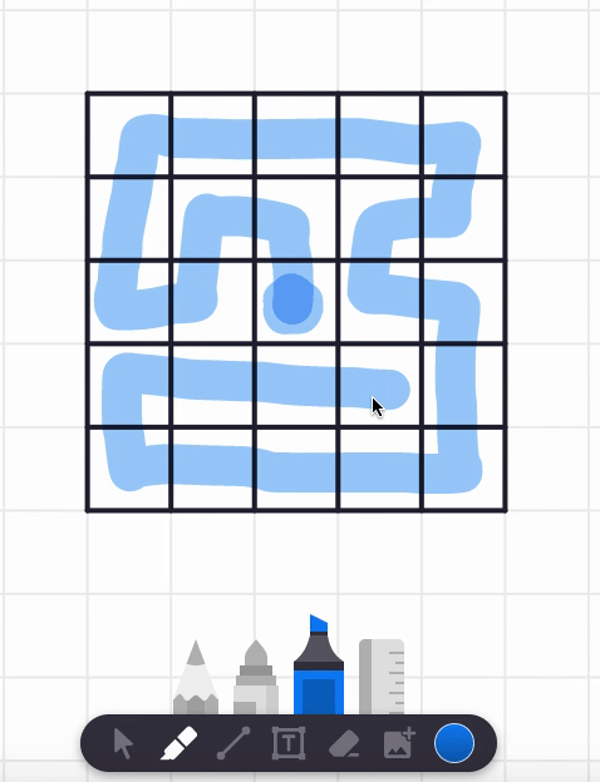
Let's try more starting points! (I certainly did when I was a kid!)
Can you find paths that visit each and every cell exactly once from each of these starting points?
Try these starting points too!
As you try different starting points, you may start to get a feel for what puzzled me as a child.
Here's me continuing my video story about this.
Keeping a Record of Matters
Here's how I started processing things.
Care to do the same thing as me? Color the squares in the grid yellow or blue based on whether we've quickly found a solution or not starting from that square. (Yellow = "Yes! A path is easy to find starting here." Blue = "Tricky!")
This GIF shows you how to copy the squares. A few cells have been filled in already for you.
Here's the result I got doing this. Did you get a checkerboard of yellow and blue cells too?
The Finished Colored in Square
Shall I lead you to the flash of insight that hit me about this checkerboard pattern? I suppose the answer is YES!
First count how many yellow cells there are. Then, count the number of blue cells too. Enter in the counts below.
Suppose you start a journey on a blue cell. What color cell must you walk to next? Can you see it must be a yellow cell?
And now that you are on a yellow cell, what color cell must you walk to next, no matter what choice you make?
Keep thinking this way. What colors must one visit from step-to-step of a path walking journey.
Can you figure out what goes terribly wrong by trying to start a journey on a blue cell?
Really sit with this for a while. Mathematicians are very, very good at sitting with problems at the backs of their minds for days and days, if not weeks and weeks. (Doing math in school is not at all like this, sadly!). But, if you are curious and can't wait to see what goes wrong (that's okay too!), then watch the next part of my story.
Every Question Answered is an Invitation to More!
Here is the lovely thing about mathematics: the more you think about a solved problem the more it just keeps unravelling to offer more and more play and joy and delight!
To see what I mean, look at the final part of my story.