Overview and Objective
In this lesson, students explore equivalent fractions. They use pattern blocks to represent equivalent fractions in as many ways as possible. First, they study the blocks in terms of the size relations between them. Then, they identify given fractions by exploring how to generate equivalent fractions and create them with pattern blocks.
Warm-Up
The traditional pattern blocks are under the Polygon tiles of the Polypad. If students are already familiar with the blocks, you may want to change their colors to the original one be selecting Alternate Tile Colours in the settings.
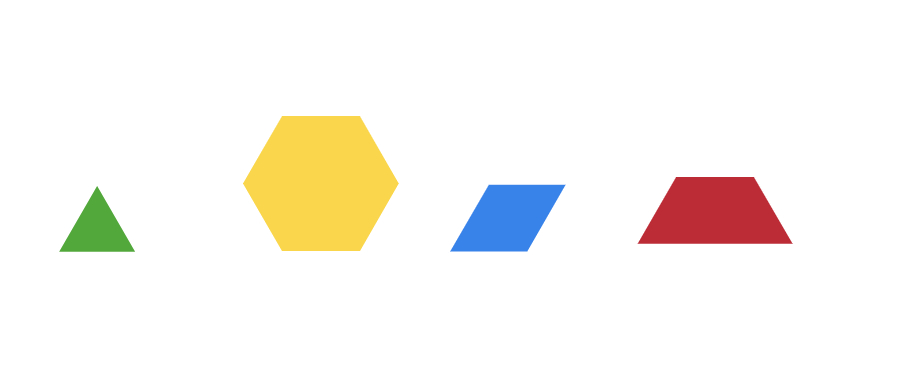
Start by inserting four pattern blocks into a blank canvas: the equilateral triangle, rhombus, trapezium, and hexagon. Invite students to copy the triangle to cover the trapezium, rhombus, and hexagon to express each in terms of the triangle. Ask students how they can represent the other blocks as numbers if they assume the triangle is 1. Invite them to make their thinking visible on the canvas. Also, ask how many rhombuses or trapeziums can be used to cover the hexagon?
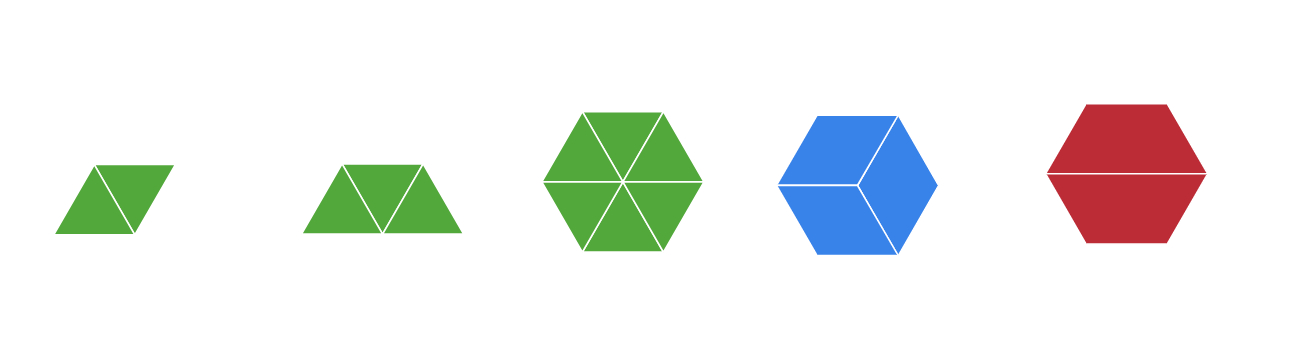
Main Activity
Share this canvas with the students and let them express each block in terms of one another.
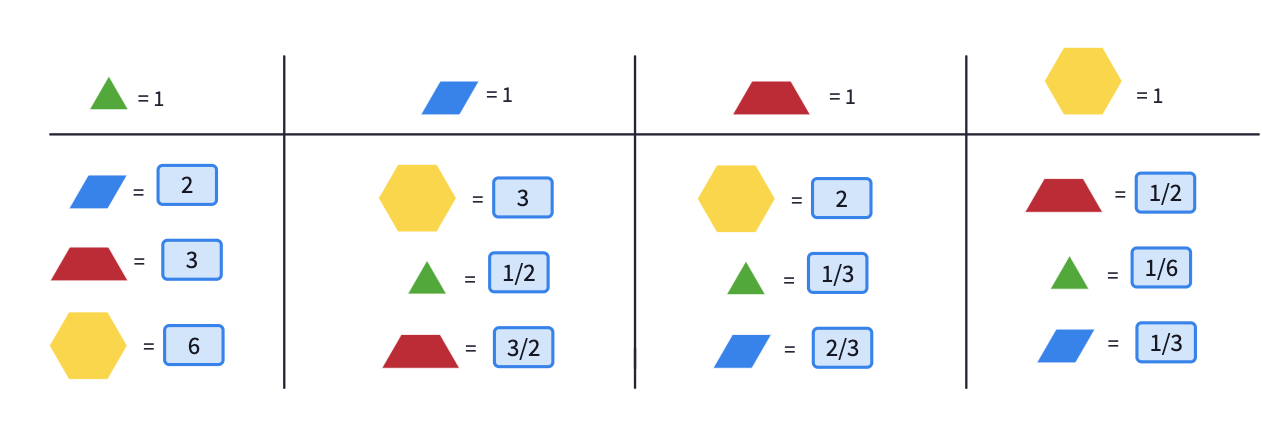
In the first part, where the triangle is assumed to be 1 unit, it is easy to express the others since we can use whole numbers to describe them. In the second section, where the rhombus is 1, students still can easily find the hexagon. Since the triangle is half of the rhombus, they might also find by intuition. Remind them to write any fraction in the answer boxes as a/b format with no space in between.
Let them work on the possible ways to express the trapezium in terms of the rhombus. Remind them to make their thinking visible on the canvas using the blocks.
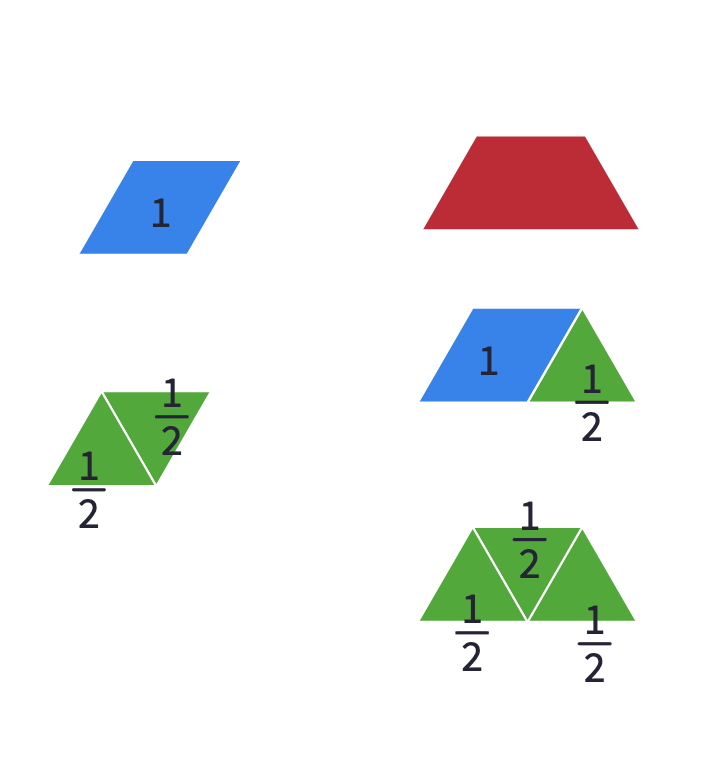
In the third section, where the trapezium is set to be 1, the hexagon and the triangle can still be found easily. Give students some time to work on the rhombus. There are many ways to find its value. Here are some possible expressions.
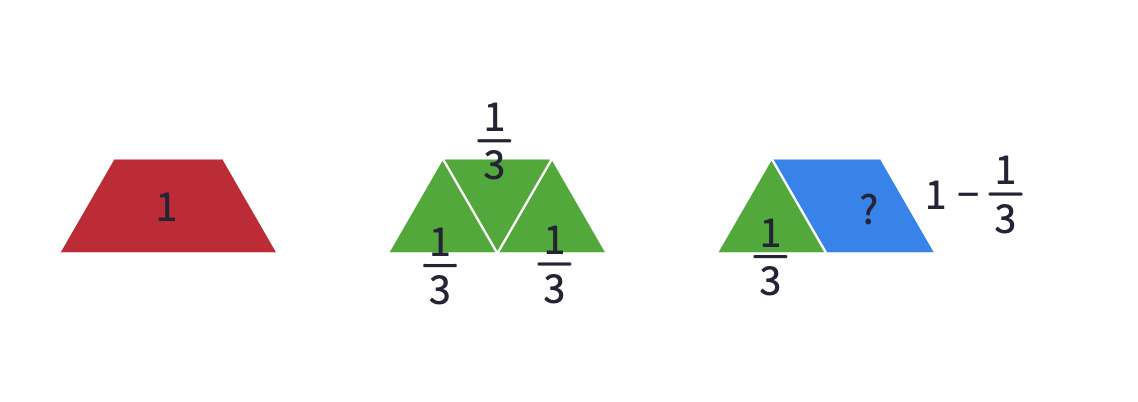
In the last section, where the hexagon is valued as 1, students can express the other blocks using unit fractions.
In the second part of the activity, share this canvas with the students. Invite students to determine what part of each shape is not yellow.
Here are some possible answers.
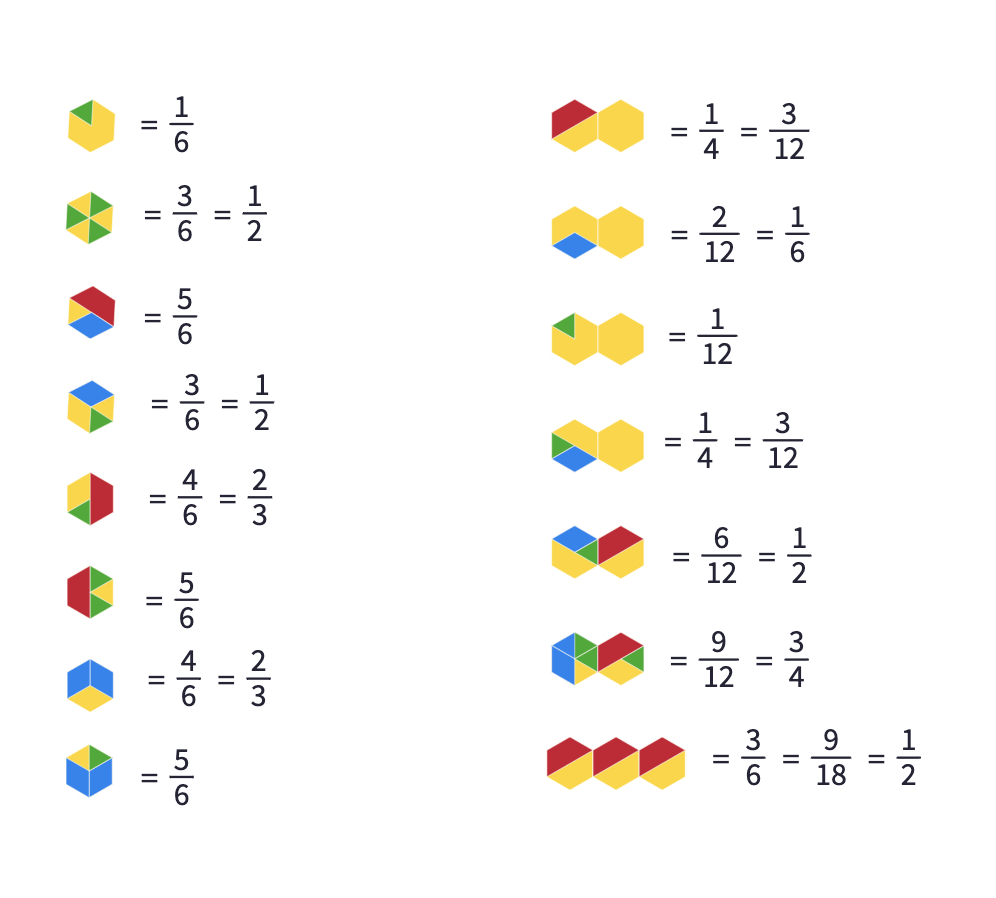
You may want to discuss the possible ways to express , both with diagrams and numbers.
Like the examples here, as long as you cover half of the hexagon, the orientation of the shapes does not matter.

Ask students to recognize all the fraction models that represent . Let them express them numerically.

and so on.
Ask students to identify other equivalent fractions on the canvas. Then, discuss the possible methods to generate more equivalent fractions and let them show using the blocks.
Closure
Share some student work with the class. Invite students to share which approaches they found most helpful when generating equivalent fractions. To close the lesson, share this canvas with students and ask them to create the given fractions in different ways using the pattern blocks.
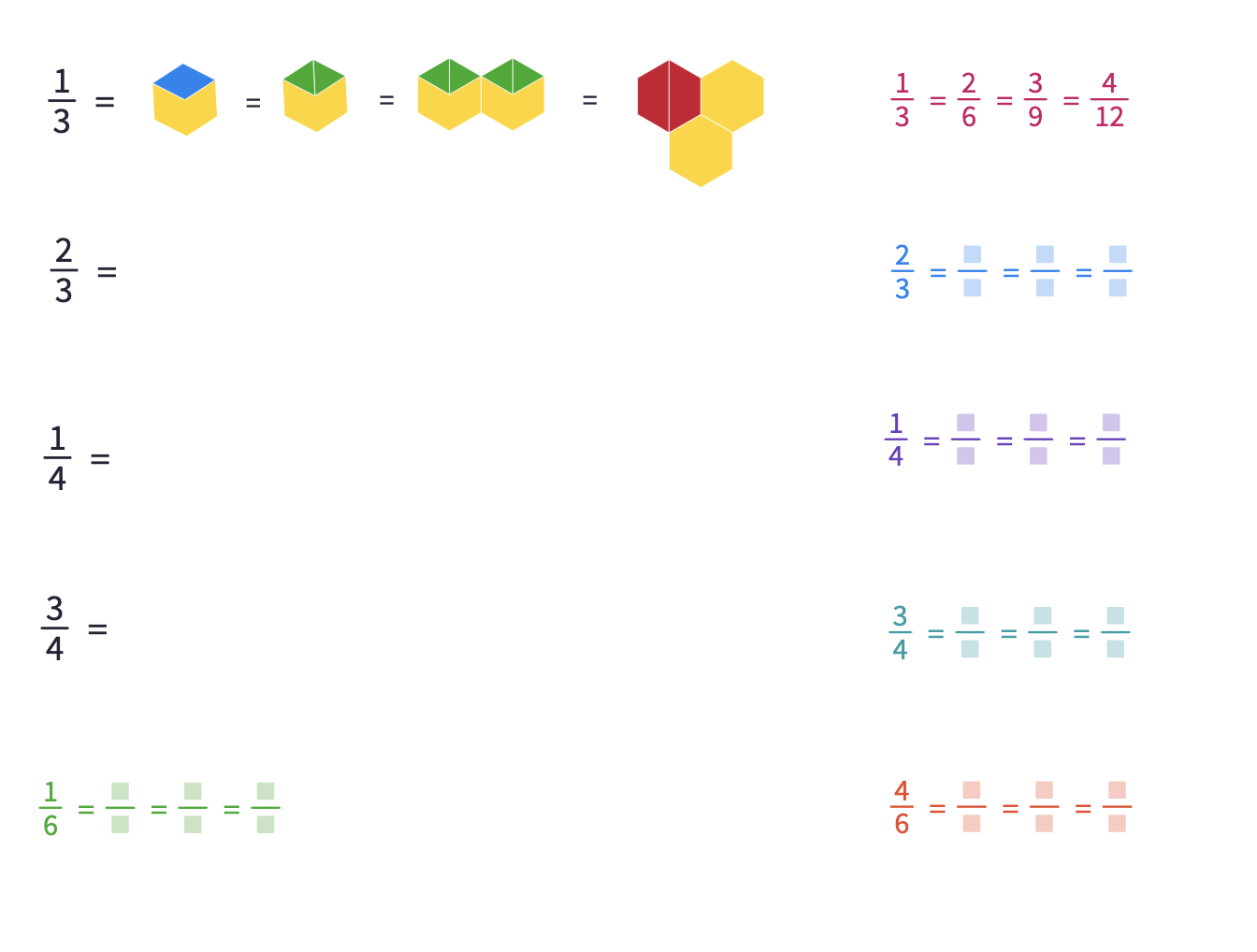
You may clarify that one can generate equivalent fractions only by multiplying or dividing the numerator and the denominator of the fraction with the same number.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account.
Click here to learn how to share Polypads with students and how to view their work.