What size squares can you make on a grid?
The vertices of the squares must be on the lattice points (grid points).
Guided Instructions:
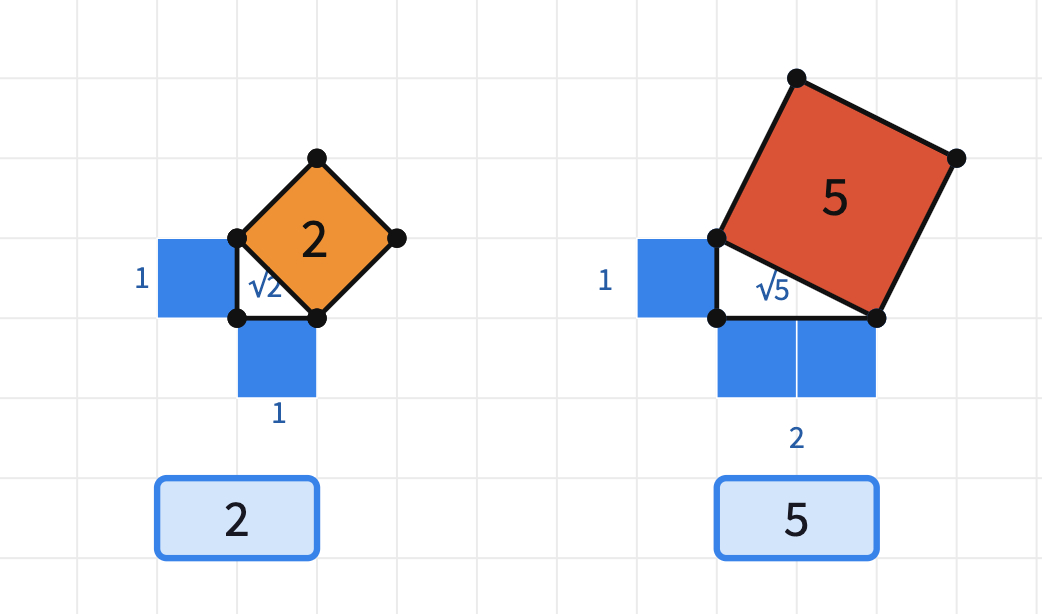
Here are some squares with the whole number of areas. Find each area in terms of unit squares.
You may recall this number sequence; 1, 4, 9, 16 ... are called square numbers. These squares are easy to find. Create at least two more squares to continue this pattern.
Try it out
Can we create other squares (maybe tilted ones) with the whole number areas?
You may have realized Pythagorean Theorem can be used to create tilted squares with the whole number areas.
Try to come up with a systematic approach to find the possible squares with the whole number areas.
Use the canvas here to create squares. Then, answer as YES/NO if you could have created squares with the areas 3, 9, 13, 27 unit squares.
Can you create a square with an area of 25 unit squares in two different ways? Are there more examples like this?
The side of a tilted square is the hypotenuse of the right-angled slope triangle, so their area is the sum of the square of the base and the height of this triangle. Now the problem is about finding all integers that can be written as the sum of two squares.
Listing your answers can help you to organize your findings.
Solutions
Here is a possibility to organise your findings:
or a table;
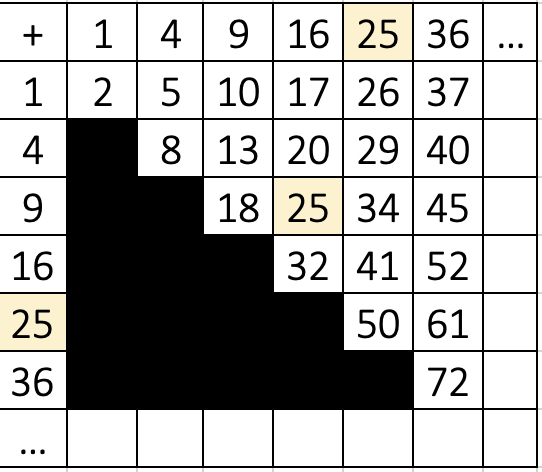
Can you find a pattern?
Are there any areas that are impossible to make? Why?
Extensions
Use the ruler tool in Polypad to estimate the irrational side length of some of the squares you have created in Part 1, such as , , and .
For example, you can rotate the square with side length units on the ruler, to read off a decimal approximation.
