Puzzle Board
A circular rosette is made by rotating circles about a fixed point and angle. Circular rosettes have a long history, going back at least 6000 years, and were popular in the Egyptian, Babylonian, Assyrian, and Greek cultures, amongst others.
To begin, explore the following relationships:
: radius of each rotating circle.
: distance between the point of rotation and the circle centers.
- If , then the rotating circles all meet at the centre of the rosette.
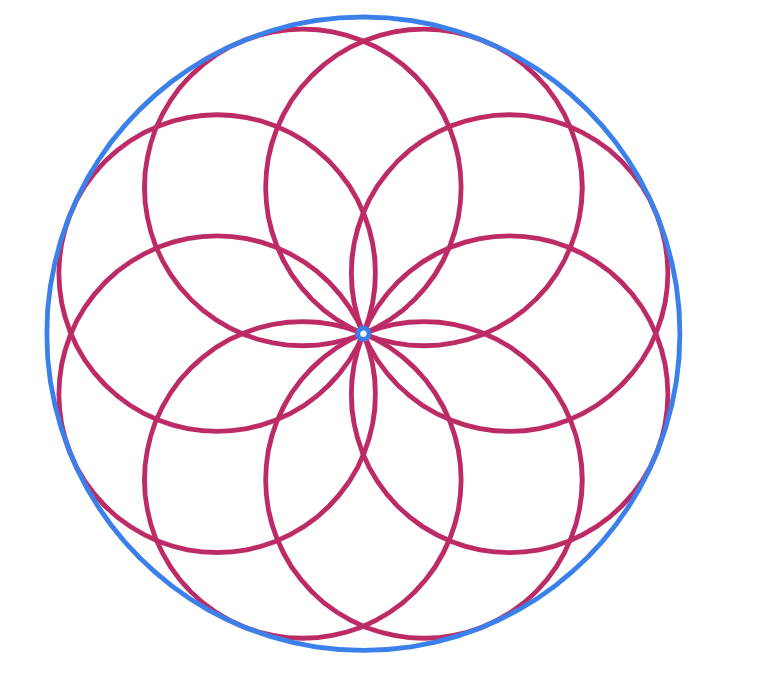
- If , then there will be a smaller hole inside the original circle.
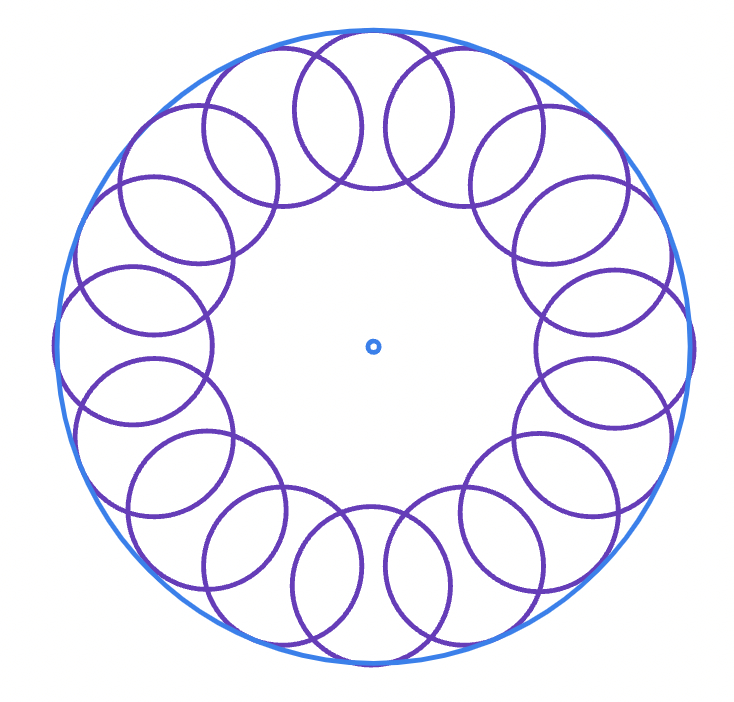
- What happens when ?
The angle of rotation of the circles determines the number of petals in the rosette.
- If the angle of rotation is 45 degrees, how many petals will the rosetta have?
- If a circular rosetta has 12 petals, what is the angle of rotation?
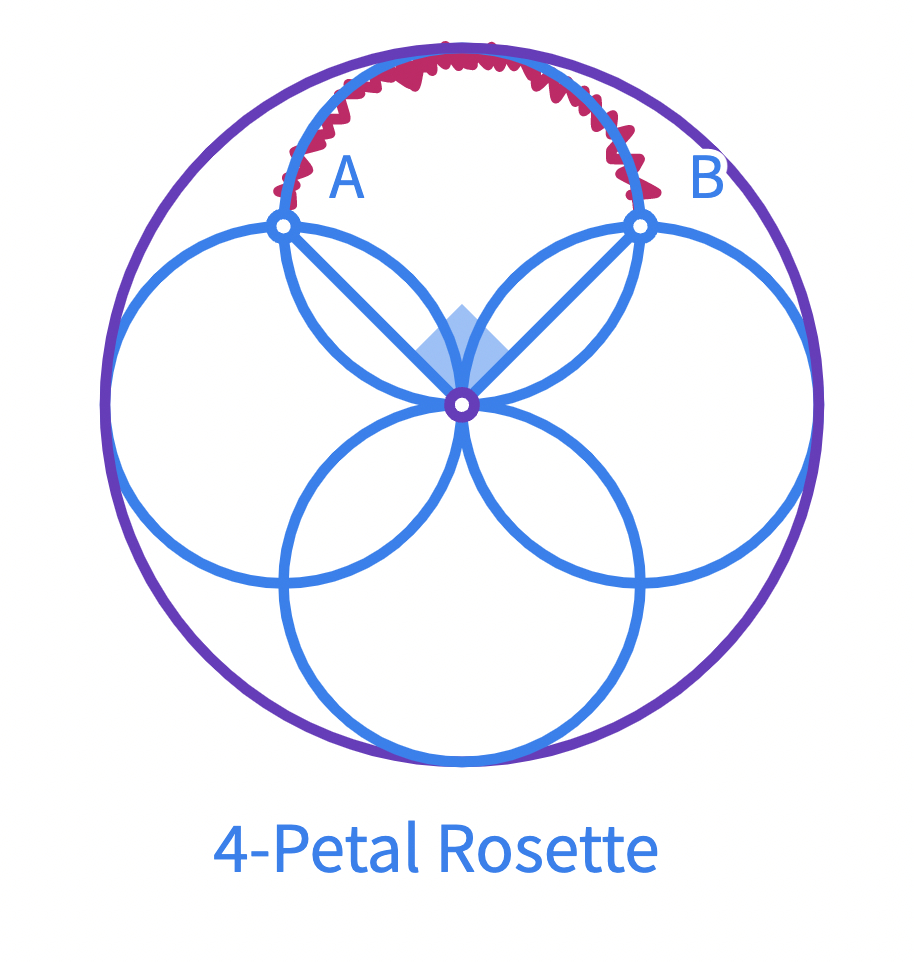
In the given 4-petals rosette where , what is the ratio of perimeter of the rosette to the circumference of the purple circle? In 6 petals? In 20 petals?
Hints
Let be the radius of the original circle and be the radius of the rotating circles.
Examing the rotation angle for the 4-petal rosette.
- Draw the segments and . if the angle between them is degrees, what can you tell about the arc-length of ?
- How many of the same AB arc does the 4 -petal rosette have?
Solution
More on
Explore the relation between the circumference of the original circle and the perimeter of the rosettes when and .