Pi in Squares and Other Shapes

Diameter Review

Below is a circle. Draw in 3 diameters. Keep reading after you've drawn in 3.

Do you remember how many diameters it takes to go around a circle?

You may recall it takes about 3.14 diameters to wrap around a circle. We use the Greek letter $\pi$ to represent this number. You can learn much more about $\pi$ in this Mathigon course.

The wheel below has a diameter of 1. Move the wheel back and forth to see the purple line unwrap from the circle.

How many $R^2$'s are needed to fill up a circle?

Let's think about squares with a side length equal to the radius of a circle.

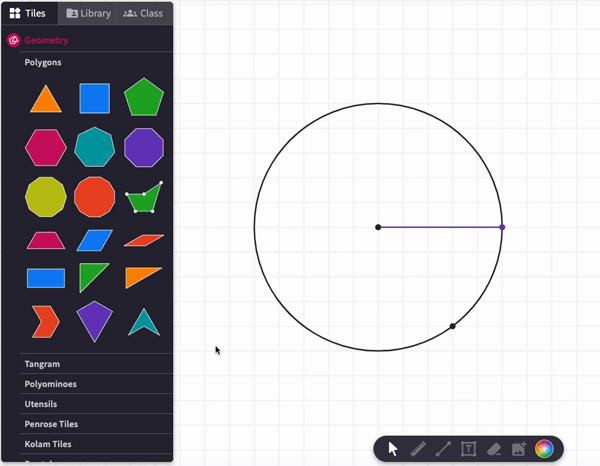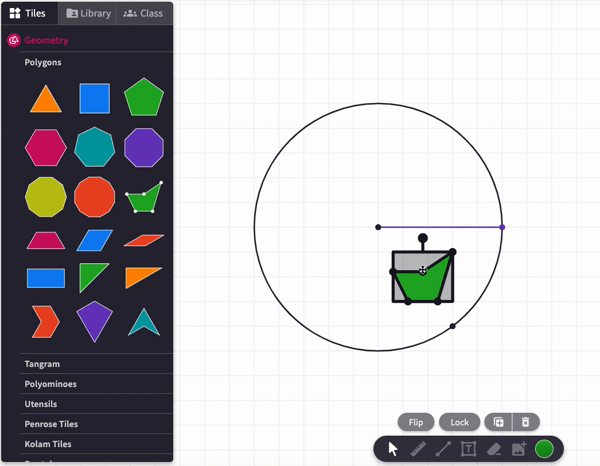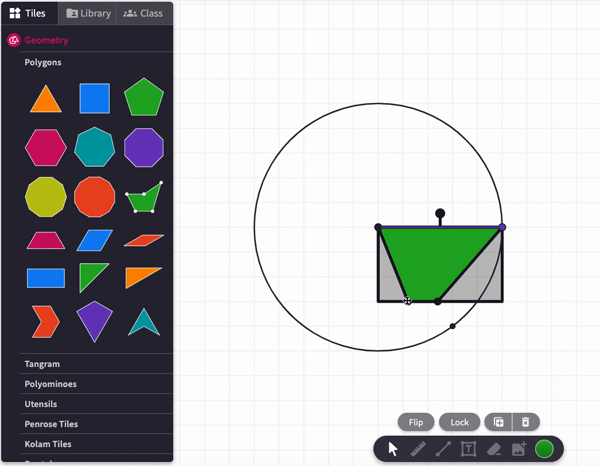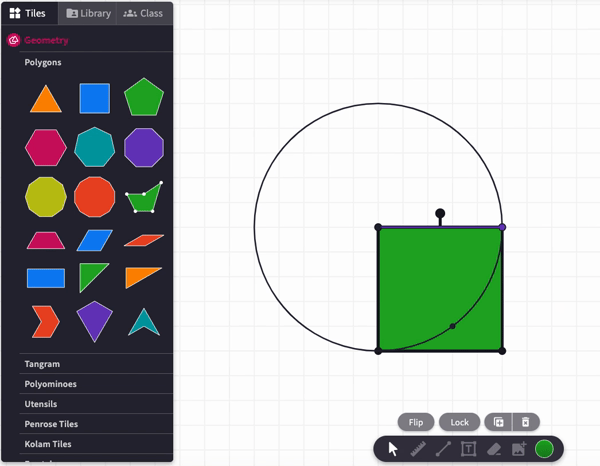
The square has a side length of R, so its area is R x R or $R^2$. How many of these $R^2$ do you think we need to fill up the circle? In the canvas below, copy squares and move them around as needed. Will 2 of them fill up the circle? 3? 4?

Move the blue pieces around to convince yourself if will take more than $2R^2$ to fill up the circle. The Flip feature may be helpful.

$4R^2$ is too many.

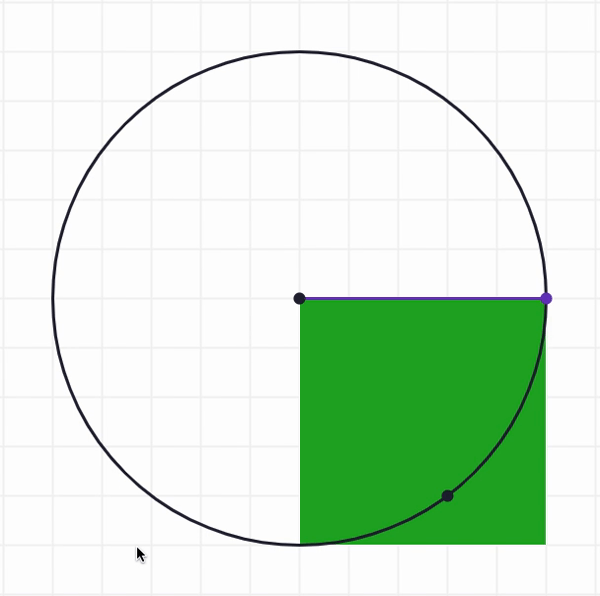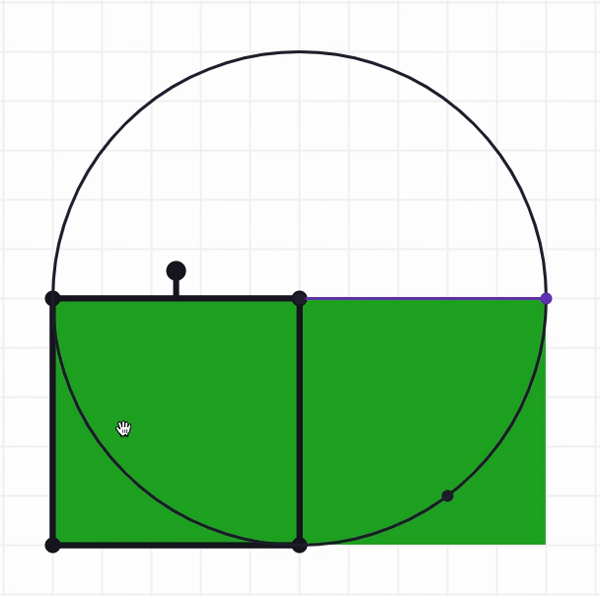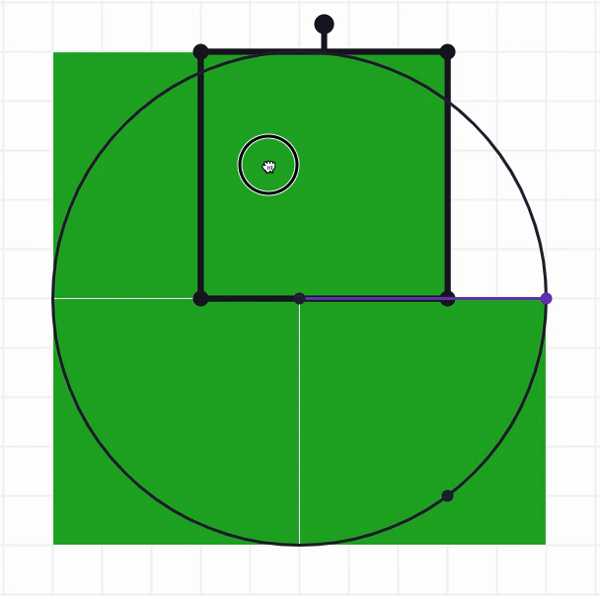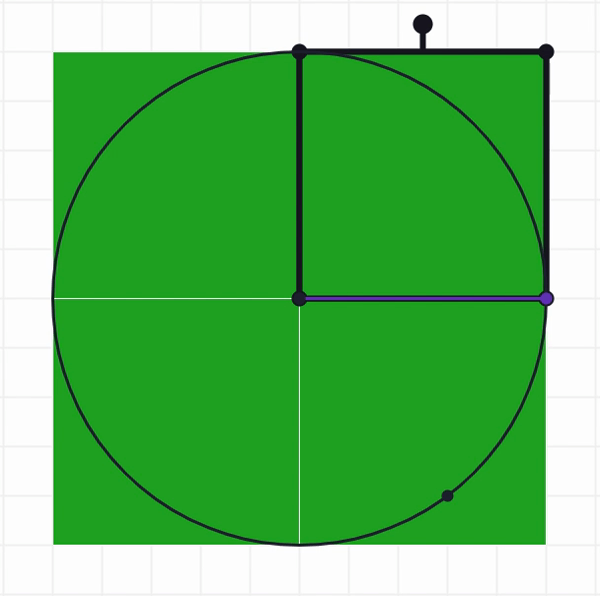
So, $2R^2$ is not enough, and $4R^2$ is too many. What about $3R^2$? We can use the Move, Flip and Cut tools to try to fill up the empty part of the circle with the blue, red, and orange regions. Below is an example of one way to start the process:

Try it out!

Here is one attempt at this process:

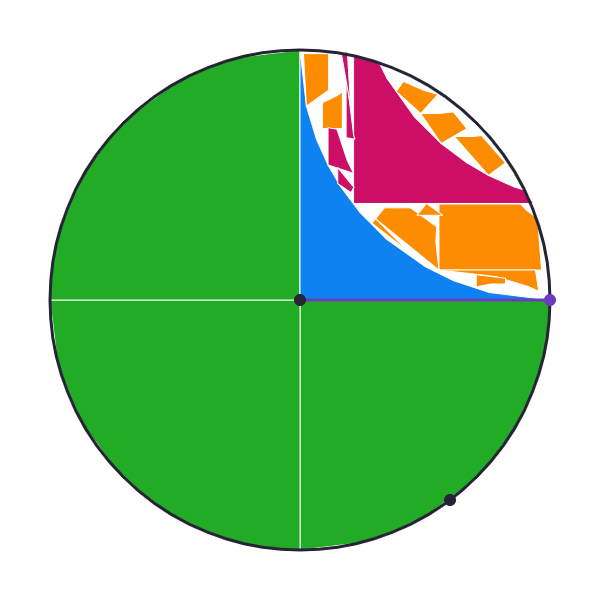
As you can see, $3R^2$ was not quite enough $R^2$s to fill up the circle. You may recall the formula for the area of a circle is $\pi R^2$. This means that it take about 3.14 $R^2$s to fill up the circle and the white space in the picture above represents about 0.14 of an $R^2$. However, this exploration has likely not convinced you it will take EXACTLY "$\pi$" $R^2$s to fill up a circle. Maybe this will help:

To conclude, not only does it take $\pi$ diameters to wrap around a circle, it also takes $\pi$ $R^2$s to fill up a circle. And $\pi \approx 3.14$

What about a Square?

What is $\pi$ for a square? Also approximately 3.14? To answer this, let's think about how many "diameters" of square does it take to go around a square and how many "$R^2$'s" does it take to fill up a square.

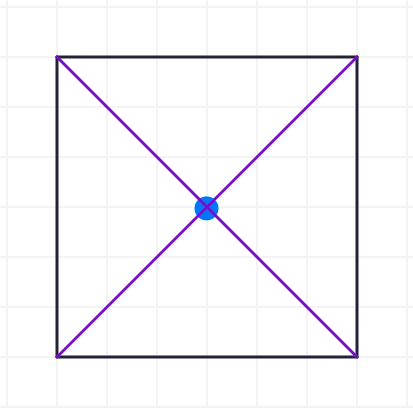
Start by drawing some diameters into the square below. Keep in mind a diameter is a straight line passing through the center of a shape.

Here are some ideas for the diameter of a square. Do any of these match up the ones you drew?

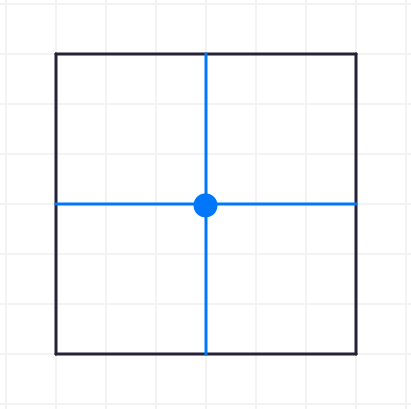
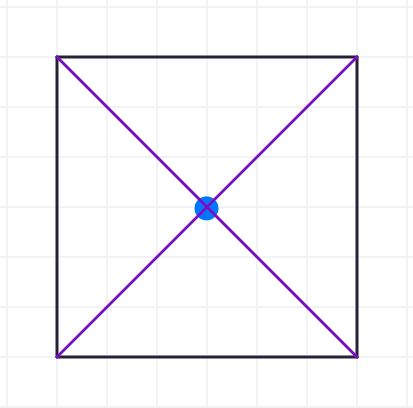
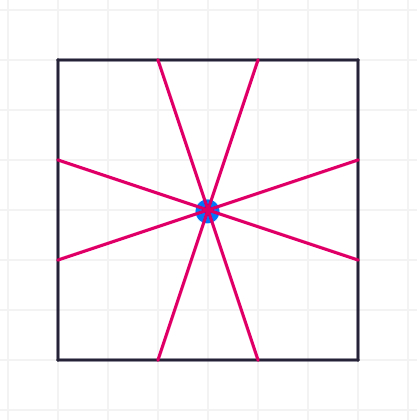
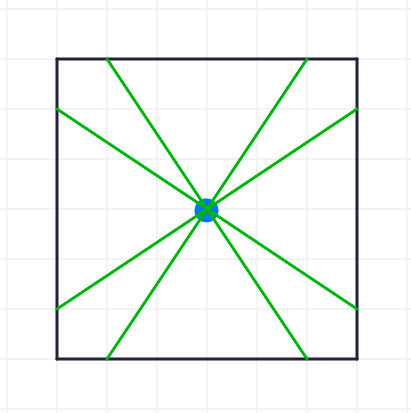
These are all great ideas. Let's explore with the first approach. How many of the BLUE diameters are needed to wrap around the square

Did you see that it took 4 of these diameters to wrap around the square?

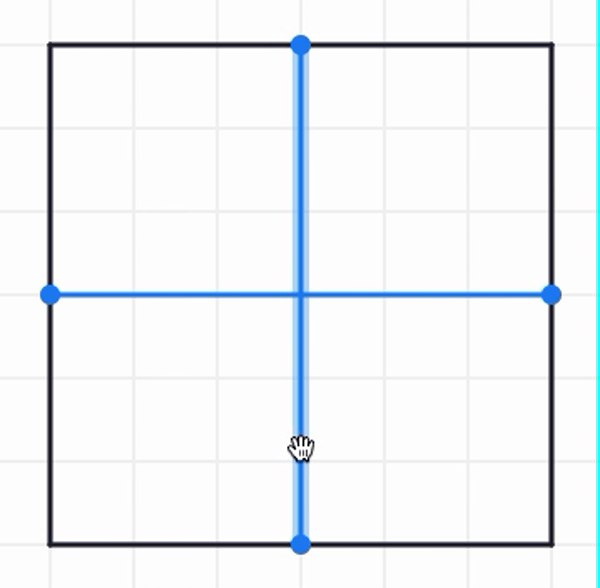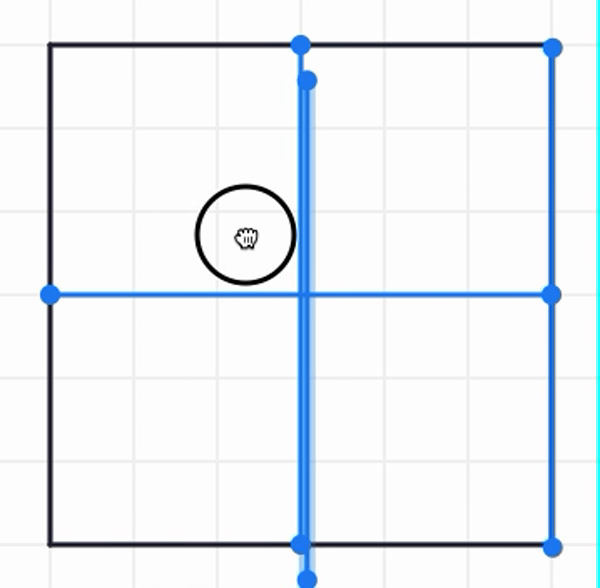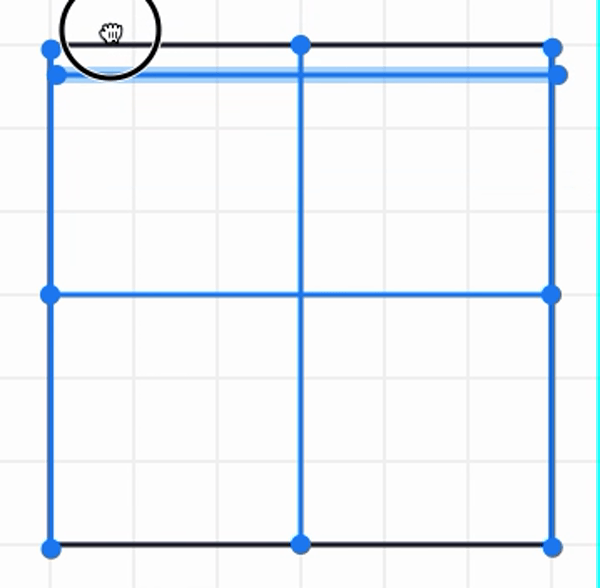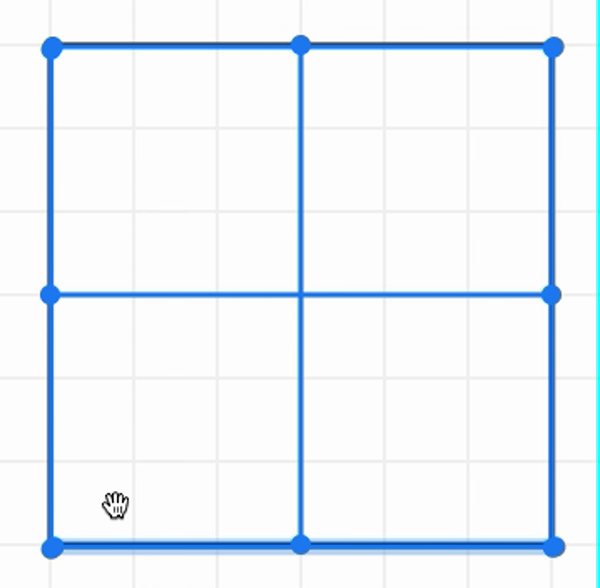
If we are thinking of the blue line as the diameter, then half of it will be the radius. The blue square below has a side length of the radius. How many of these $R^2$ does it take to fill up the big square?

When we use the blue line as the diameter, it takes 4 diameters to wrap around the square and 4 $R^2$s to fill up the square. So, in this case, $\pi$ seems to equal 4.

Here is a summary of our work so far:

• In a circle, about 3.14 diameters wrap around the circle and about 3.14 $R^2$s fill up the circle.
• In a square, 4 diameters wrap around the square and 4 $R^2$s fill up the square.

This is very exciting! We have found that the value of $\pi$ for a square seems to be 4!

What about the other possible diameters?

What if we used a different diameter for the square?

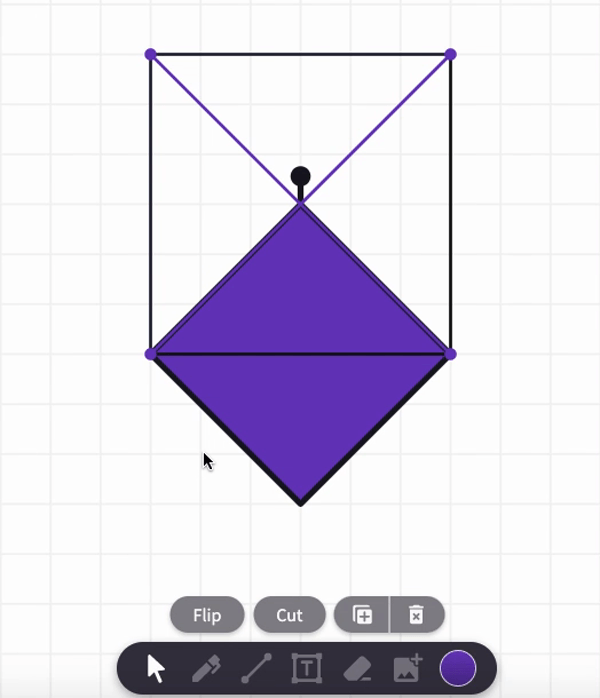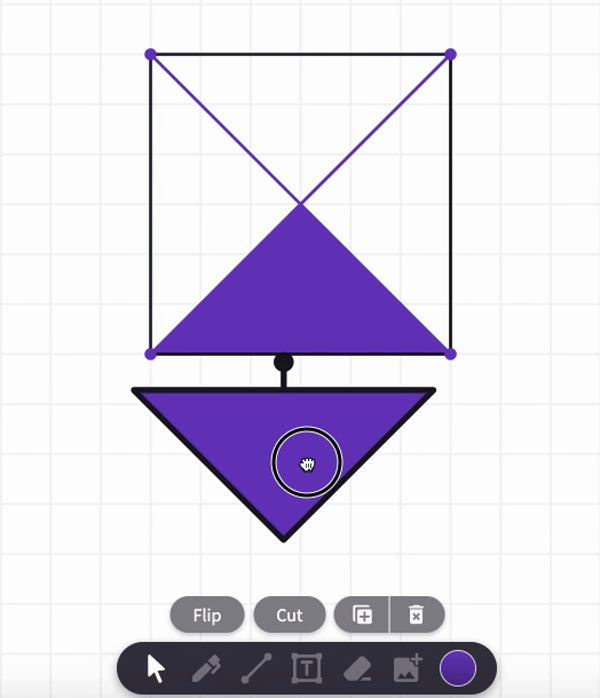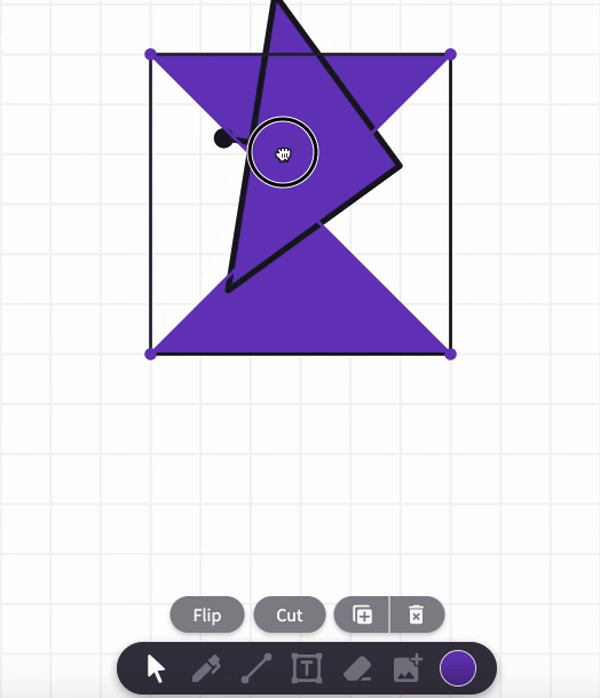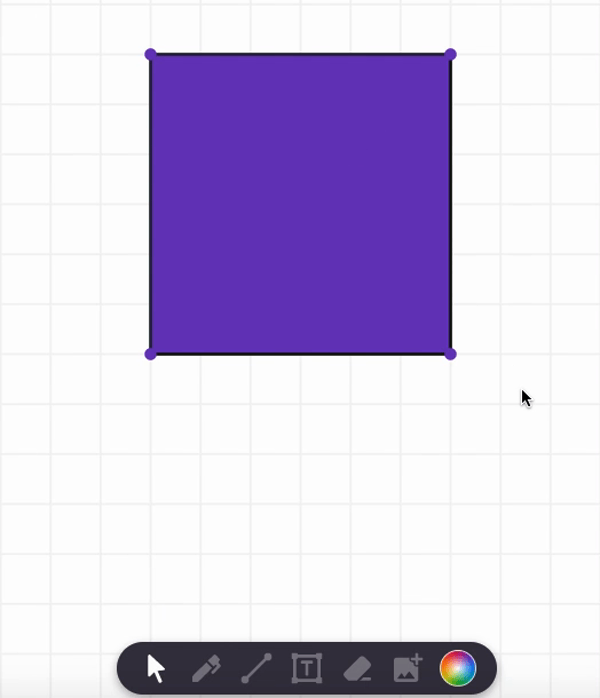
How many of these purple diameters will it take to wrap around the square? Use the ruler to measure the diameter. Then answer the questions. Round answers to the tenths place as needed.

The perimeter is 24 and the purple diameter is about 8.5. So, it will take about 2.8 diameters to wrap around the square

Now, let's see how many $R^2$ it will take to fill up the square when we use the purple diameter. Copy, move, and cut the purples square as needed to fill up the big square.

You may have found it took 2 of these purple $R^2$s to fill up the square:

So, Which Diameter?

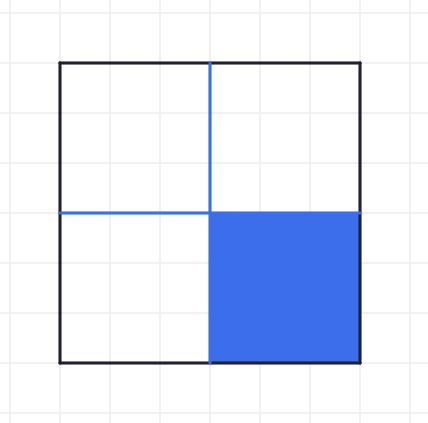
4 of the BLUE diameters are needed to wrap around the square and 4 of the BLUE $R^2$s are needed to fill the square.

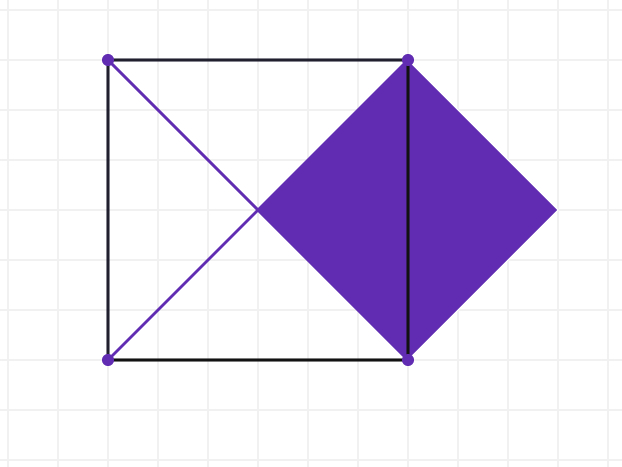
2.8 of the PURPLE diameters are needed to wrap around the square, but only 2 of the PURPLE $R^2$s are needed to fill the square.

The choices we make for the "diameter" of a square impact whether or not we end up with the same number for each interpretation for $\pi$ in a square. Based on these two choices, which one - the blue one or the purple one - would you like to think of as the diameter of a square? We'll end here with this question for you to think about!

Extend Your Work

• What will happen if we use some of these as the diameter of the square? Is there another diameter for which the two ways to think about $\pi$ will give the same number?

• Is there a "diameter" you can find for this rectangle that will result in the same values for both ways we've been thinking about $\pi$?

• Can you try a similar analysis in other regular polygons?