Overview and Objective
In this lesson, students will use the geared clock on Polypad to explore the angles made by the hour and minute hands of an analog clock.
Warm-Up
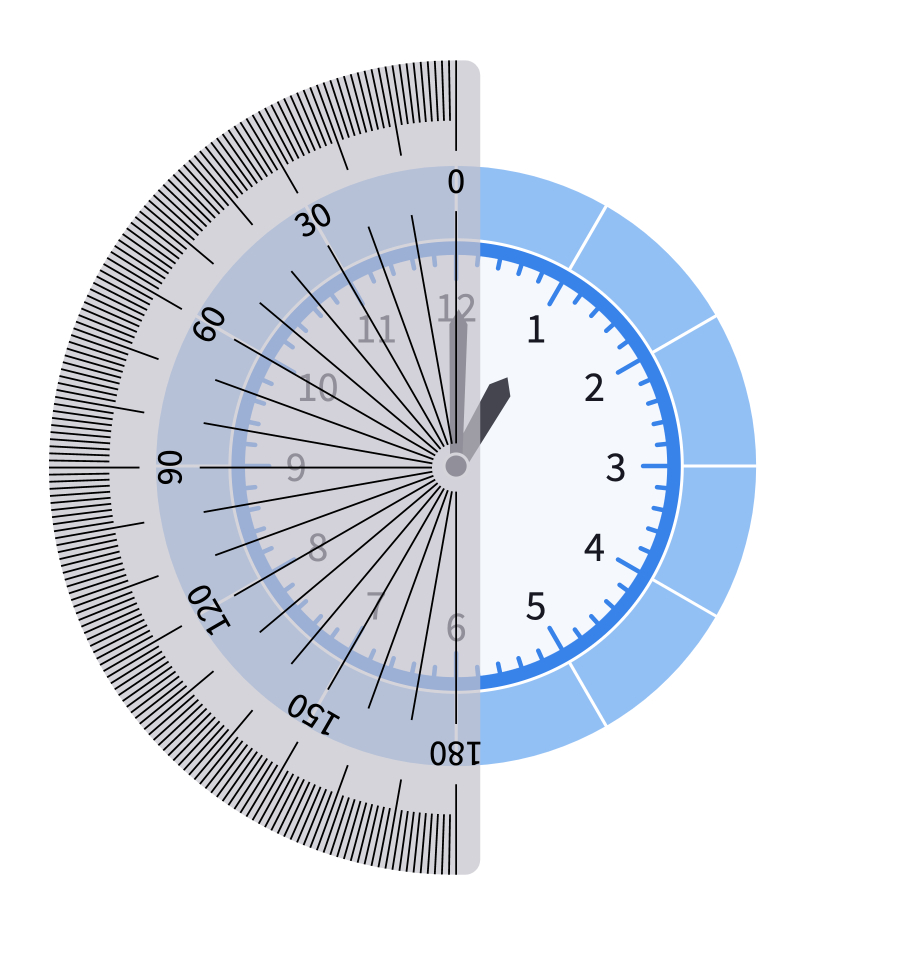
Start by discussing with students the angle of a full turn. Share this canvas with students and invite them to determine the angle measurement between two consecutive minutes and the angle measurement between two consecutive hours. There is a 6-degree angle between the minutes and there is a 30-degree angle between the marks of two consecutive hours.
You may also use the fraction slice of to create each 30-degree angle.
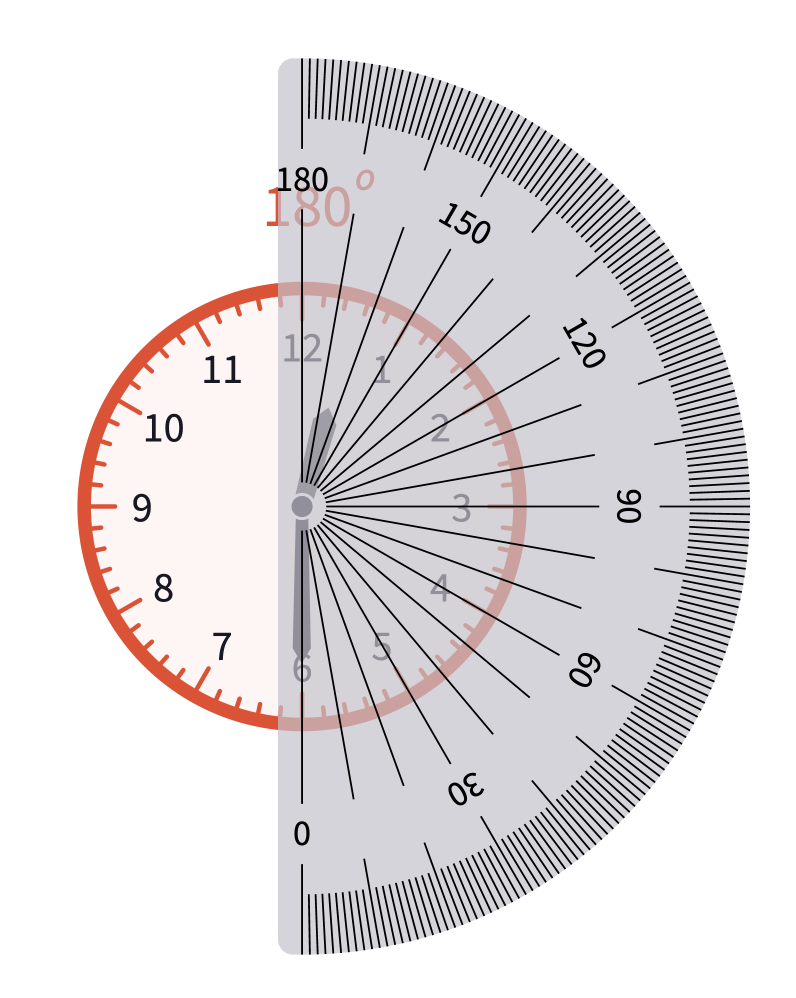
Ask students to create a straight angle by arranging the hour and minute hands of the red clock. Let them share their answers.
Clarify with the students that It doesn't matter whether it is 6 am or 6 pm; the angle is the same, , for both. (The easiest answer is 6:00, but since the hands turn smoothly, it will happen 11 more times in 12 hours.)
Discuss if 12:30 creates a straight angle or not. You can use the protractor tool to make a demonstration or let them measure on their own. You may use the same method to disprove 3:45 or 9:15.
On the same canvas, ask students to create the angles of , , and using the hands of the hour and minute of given geared clocks*.
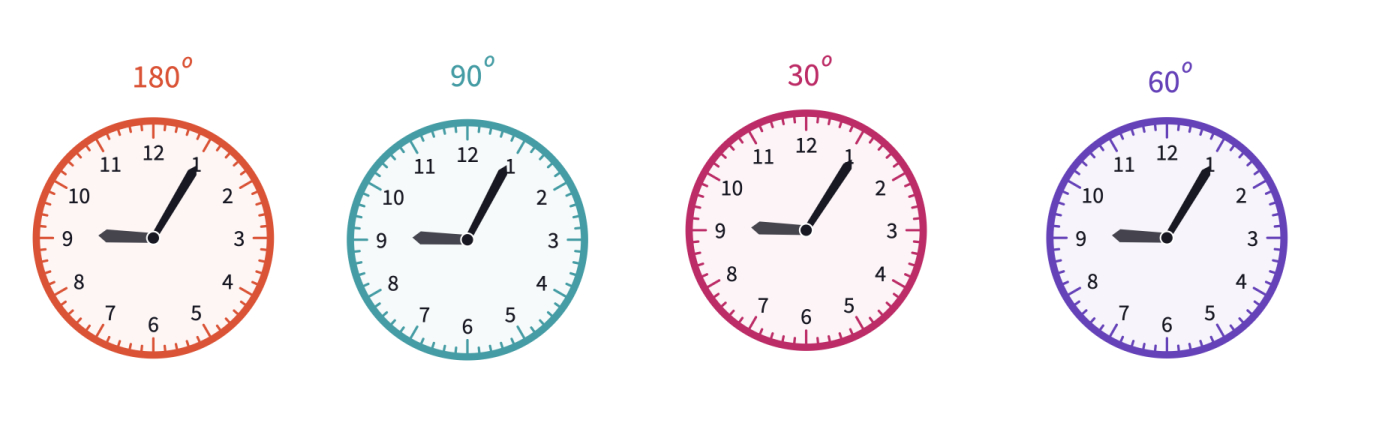
You can use the toggle seconds option at the bottom center toolbar after selecting a clock on the canvas to hide and show the second hand. The given clocks only show the hour and minute hands for students to measure the angles without confusion.
There are many possible answers to these questions. At this point, we will concentrate on the ones that are easy to find, like 1:00 or 11:00 for 30 degrees or 3:00 and 9:00 for 90 degrees.
Main Activity
Use the demonstration canvas to ask students the (smaller) angle between the hour and minute hands of the clock at 2:30. Start with asking students where each hand points out at 2:30.

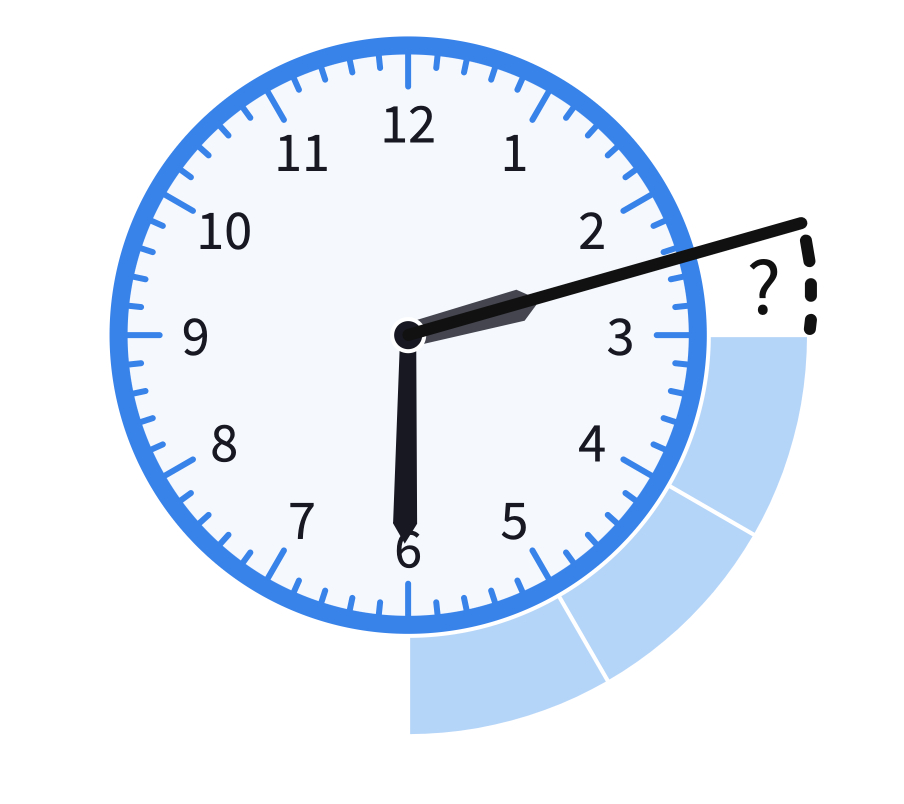
Discuss with students that at 2:30, the minute hand points to 6 and the hour hand points halfway between the 2 and the 3.
You can use the fraction slice of to mark each full angle between the hands. We have 3 lots of and a half of . So the total angle is x = .
You may then ask about 12:30, which shows on the clock.

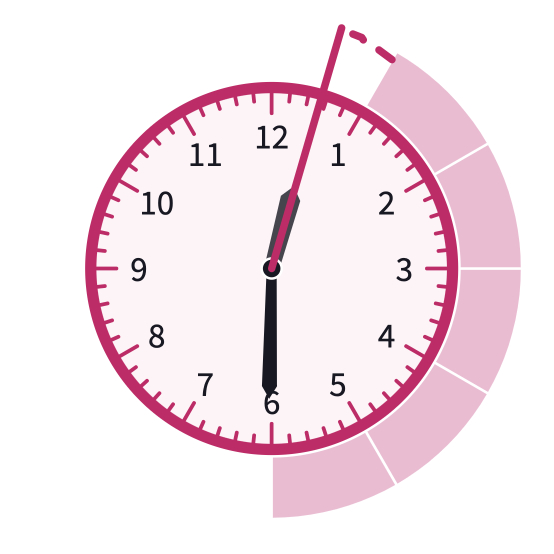
After students have an initial understanding of the angles created by the hour hand in relation to the minute hand, share this canvas with students and allow students time to work on the angle at 10:15.
Take some time to talk about possible steps, perhaps using the following prompts for discussion.
- How many full 30 degrees lots are there between the hands?
- Where the hour hand points exactly considering the minute hand covered 15 minutes of its 60-minute cycle?

Clarify with the students that the hour hand is of the way from "10" to "11". Therefore the angle between 11 and where the hour hand points is of .
x so the total angle is x degrees.
You might like to encourage students to estimate the angles before they calculate so that they can check if their final answers make sense.
The next question on the canvas is 6:45. Discuss where each hand points out at 6:45. Students need to be able to comment that hour hand is at of the way between 6 and 7. So, we need to calculate of 30 degrees to find the angle between the hands.
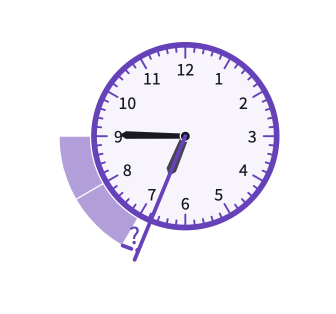
x . So, the total angle is x degrees. They can use the protractor to measure the angle.
According to the needs of students, you may increase the number of examples with the quarter and half hours. Then, if the students are ready for more complicated questions, you can move on to the next clocks on the canvas.

Closure
Share some student work with the class. Invite students to share which approaches they found most useful when answering these questions. To close the lesson, you may group students as pairs and share this canvas to ask the angle between the clock hands at 01:36.

Support and Extension
For students ready for additional extension in this lesson, consider asking questions like finding the angle at 1:33 or 11:57. You may also ask them to find a time that has 180 degrees between the hour and minute hands other than 6:00 o'clock.
For students needing additional support with these ideas, you can increase the number of examples for each benchmark question.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account.
Click here to learn how to share Polypads with students and how to view their work.