Overview and Objective
In this activity, students use algebraic expressions to write a general formula for the sum of the numbers covered by tetrominoes. Then, they will use different size number grids to explore the relationship between the grid size and the algebraic expression representing the sum of each tetromino.
Warm-Up
If students have not seen tetrominoes before, introduce them and talk about the number of squares they cover. For this lesson, rather than using the premade tetrominoes in the Geometry menu on Polypad, students will use custom tetrominoes. This is needed to match the size of the number grids.
Place the students in pairs or groups of three and share this canvas. Click here to learn how to share Polypads with students and how to view their work.

Tetromino Sum Game
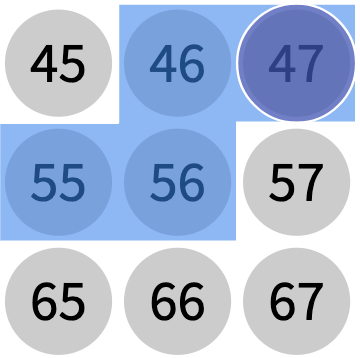
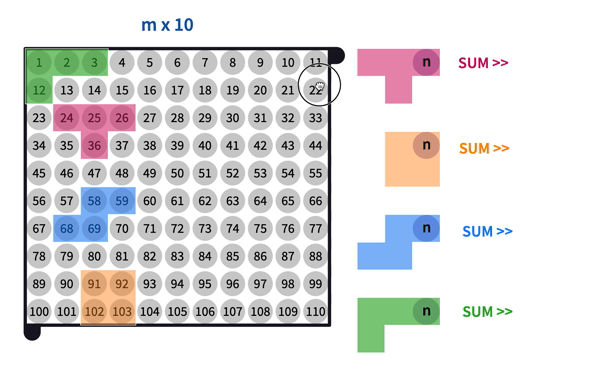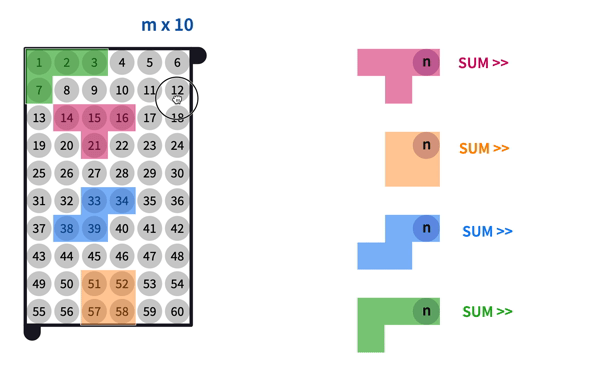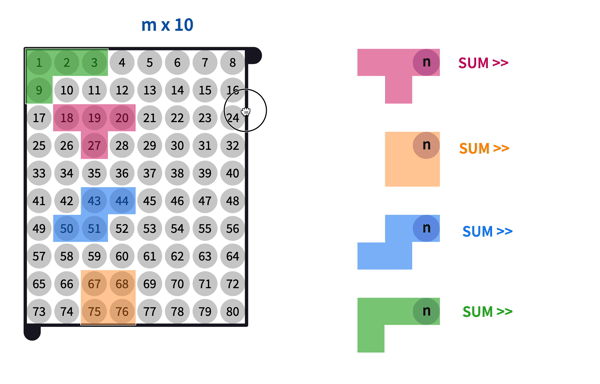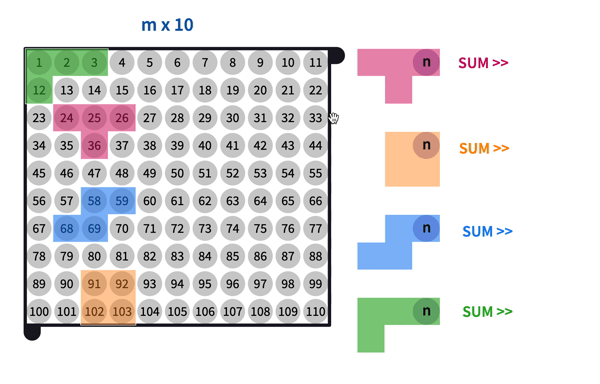
Students place the tetrominoes anywhere on the 10 x 10 number grid without changing the orientation. Then, they find the sums of the four covered numbers and share that sum with a classmate. Students try to determine the numbers covered by the 4 tetrominoes. Model one example with the class.
After a few minutes, ask some students to share their sums with the class. You can then use the algebraic rules below to find the students' numbers. This creates some wow-factor and intrigue for the students.
Here are the algebraic rules to find the numbers covered by tetrominoes on the 10 x 10 Number Grid in terms of the upper-right number "n". Do not share these yet with students. They will try to determine them for themselves in the next part of the lesson.
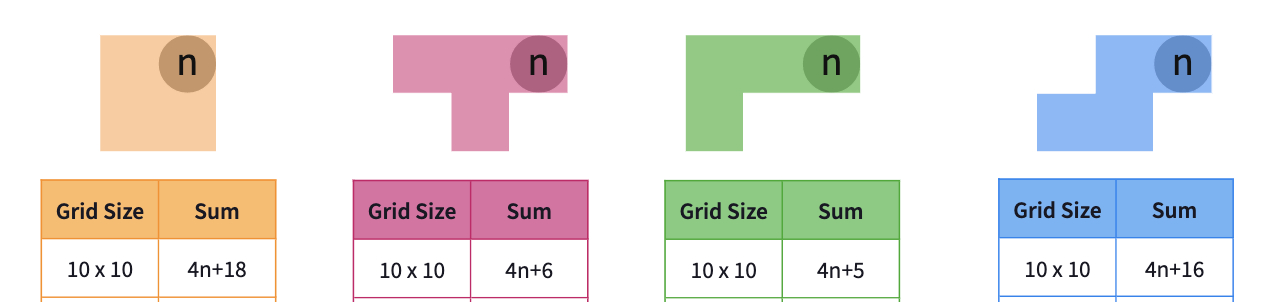
Alternative Warm-Up
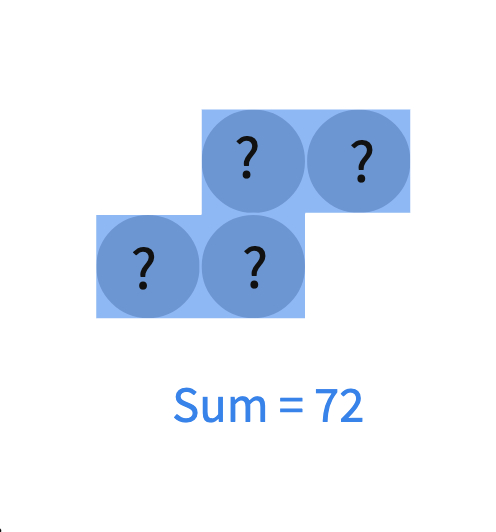
As an alternative warm-up, you may group the students as pairs and have them play a guessing game by sharing this canvas
Main Activity
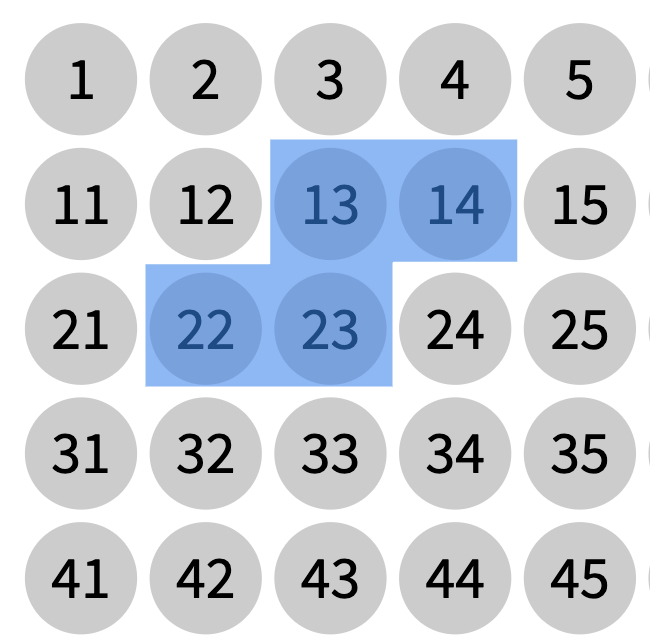
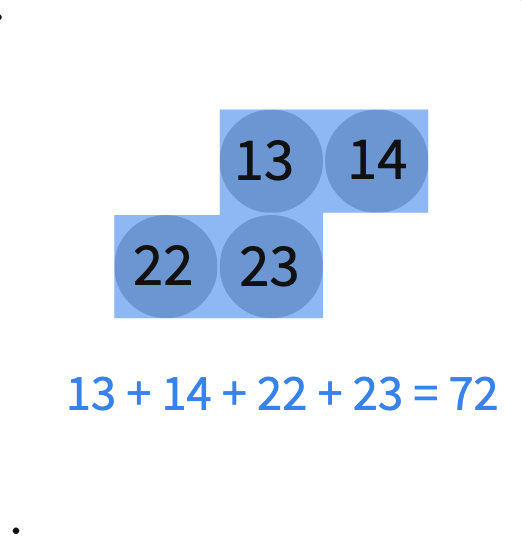
In this part of the lesson, students will work towards developing an algebraic expression for each tetromino. Depending on the background of your students, you may want to work on one together as a class first and then have them work on their own. Below is an example of how you can use the algebra tiles to determine the expression for the blue piece.
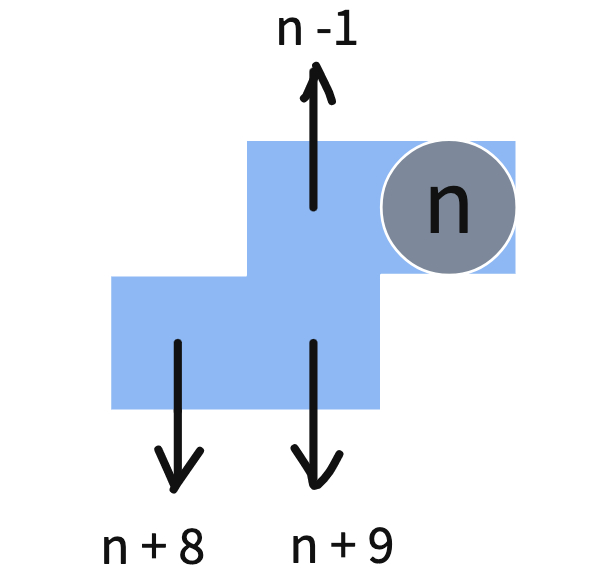
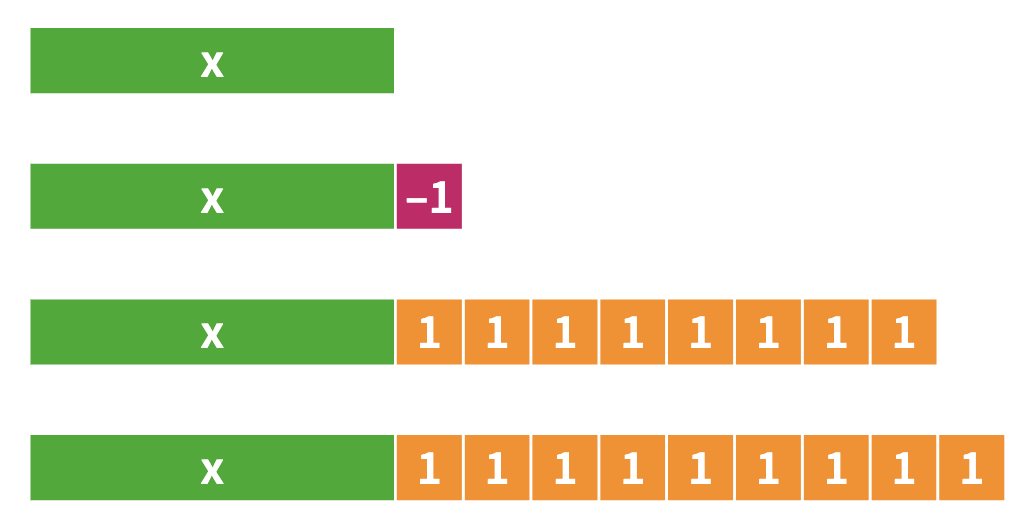
Once students have found the correct expressions for the pieces in the 10 x 10 grid, have students share some solutions with the class. Some students may have different, correct expressions depending on their starting position of the variable. This can lead to a good conversation of defining the variable before beginning. Below is one position of "n", but certainly any starting position can work.
Next, ask them if they think the expressions will change if they change the size of the grid. Send them back to work individually or in pairs and encourage them to check their predictions by changing the size of the grid using the black tabs and using their expressions to find the new sums.

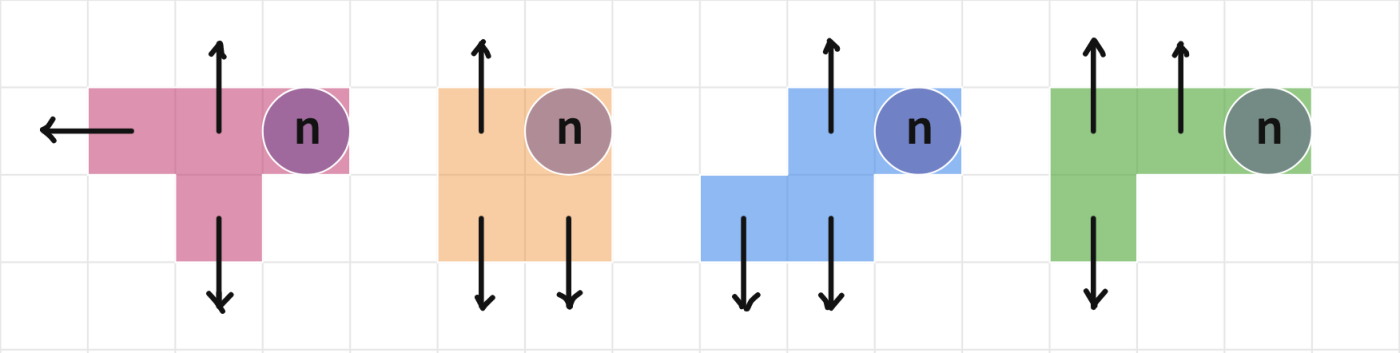
They will find their expressions no longer work. Invite them to find the new expressions for a different sized grid and record their results in an organized manner so they can share them later with the class. Remind students to keep the orientation of tetrominoes the same. Depending on your preference, you can either let students explore any size grid they like, or assign them to work on a 6 x 10 grid and a 16 x 10 grid. As students are working, remind them to keep track of their results. You may want to encourage them to use the table in Polypad to organize their work.
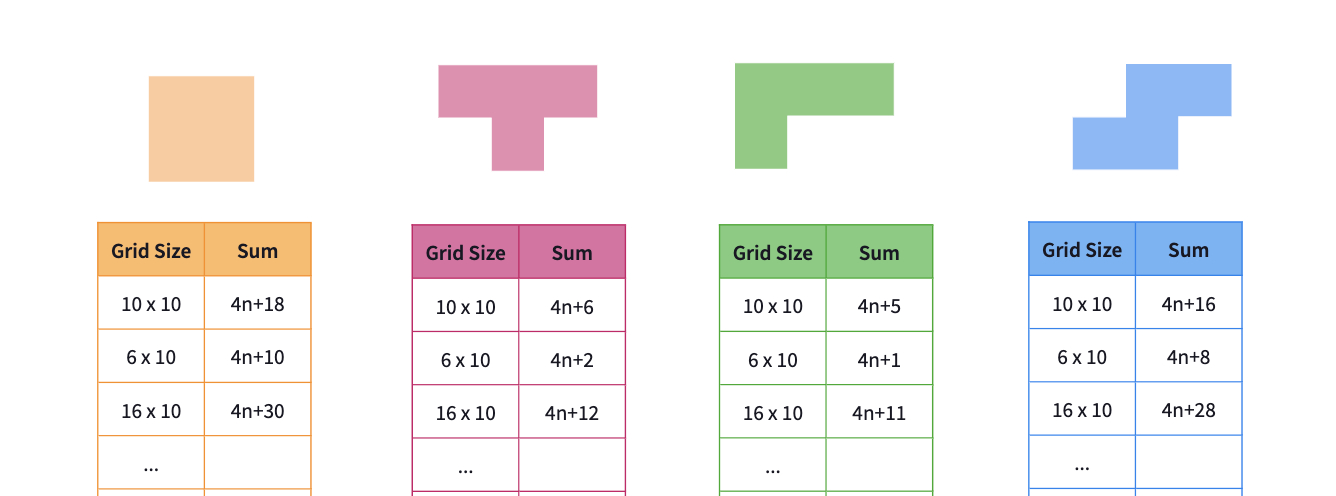
After some work time, share some student work with the class and talk about the similar patterns they observe in different number grids. You may want to make one class version of the tables above and record all solutions. Here are some questions to discuss together:
- How did the numbers in the same row with the number labeled as n change in different number grids?
- How did the numbers in the row below of 'n' change?
- How can we express the sums for each tetromino in a 7 x 10 grid?
- Is there a relationship between the number sum of each tetromino and the size of the grid?
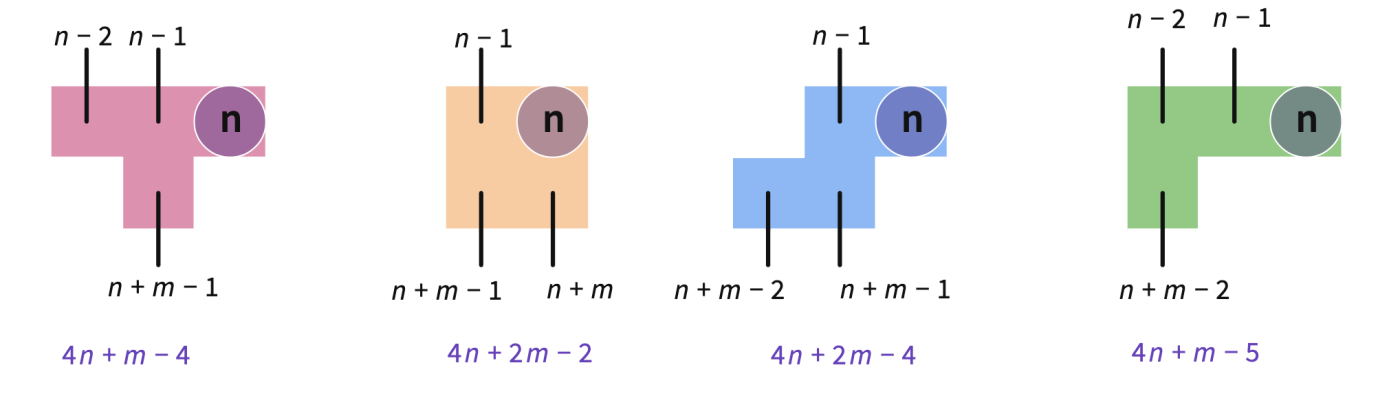
Some students may start to grasp the relation between the size of the number grid and the number sums. You may ask them to predict the sums for an 'm by 10' number grid. After noting down the predictions, ask the tetromino sums for an 'm x 10' number grid.
Clarify with students that the top row numbers are still expressed as and . The numbers in the bottom row can be written by using two variables now.
Some possible answers here can be
Alternative Activity
For a more structured lesson, share this Polypad canvas with students. This canvas contains the 10 x 10, 6 x 10, and 16 x 10 number grids all together so students can work through the progression of the lesson on their own.
Closure
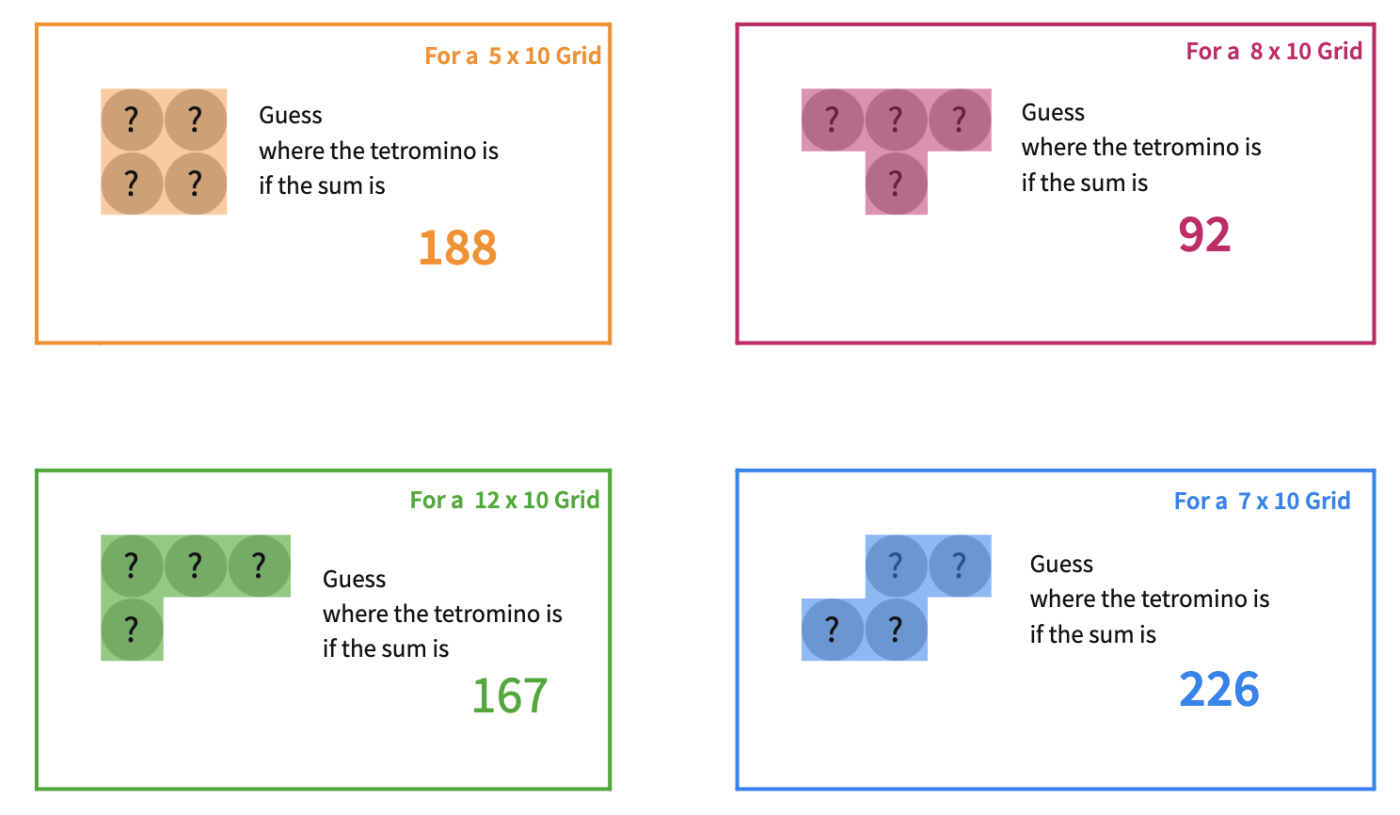
To close the lesson, discuss the advantages of simplifying expressions by combining like terms. You can also (re)play the guessing game. Now, students can use the general formulas for the sums to find the place of the tetrominoes on the grid. You can now discuss how you found their numbers at the start of class.
Support and Extension
For students needing additional support with expressing numbers in terms of n, use more examples with small numbers to allow them to see the relations easier.
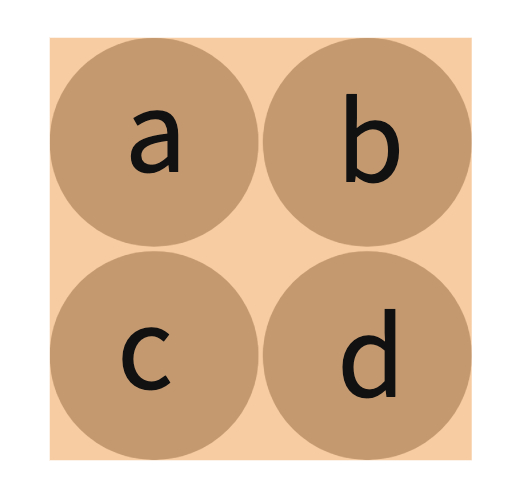
= ?
Encourage students to try numerical examples in different size of number grids to reach the conclusion "m" for a 'm by 10' number grid. Then they may try to prove this result using algebra.