Main Activity
Suppose we want to build a brick wall out of the usual size of a brick which has a length of 2 units and a height of 1 unit.

If our wall is to be 2 units tall, we can build our wall in a number of different ways depending on how long we want to build it. Our problem here is to find the number of ways that we can build a 10 units long wall.
Use the canvas here to study the problem:
We may start solving the problem by arranging the bricks for a 2 x 1 rectangle first.
How many possible ways can they be laid?
Next, look at the 2 x 2 construction.
How many arrangements are possible?
Now try 2 x 3 arrangements.
Before we work our way up to the 2 x 10. Let’s try to see if any particular pattern starting to emerge?
Solution
The tricky pattern to spot is that each total on the right is the sum of the previous two totals.
- 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
You may have heard of the Fibonacci numbers will notice that the totals are the Fibonacci sequence, starting at 1, 2, …
So by following the Fibonacci Sequence, for the 10-unit long wall; there are 89 possible ways to arrange the bricks
You may read more about Fibonacci Numbers on Mathigon
Extension
We may wonder in how many different ways can we build an “n” unit-long wall.
In fact, there is a formula for finding any Fibonacci number without having to add up all the previous ones.
If we go back to the first question, for the 10-unit-long wall;
the number with 5 pairs lengthwise and no slabs across the path (just 1 way)= 5 choose 5

the number with 4 pairs lengthwise and 2 across (15 ways)= 6 choose 4

the number with 3 pairs lengthwise and 4 across (35 ways)= 7 choose 3
the number with 2 pairs lengthwise and 6 across (28 ways)= 8 choose 2
the number with one pair lengthwise and 8 across (9 ways) = 9 choose 1
and the number with no pairs lengthwise and all 10 across (1 way) = 10 choose 0
So the total number of ways is
C(10,0) + C(9,1) + C(8,2) + C(7,3) + C(6,4) + C(5,5)
1 + 9 + 28 + 35 + 15 + 1 = 89
We may see these numbers on the Pascal Triangle in a diagonal format.

So for n unit long wall, we can use the combination idea to choose the lengthwise bricks from a total of n bricks.
The total number of ways:
C(n,0) + C(n-1,1)+ C(n-2,2)+ C(n-3,3)+ C(n-4,4) ...+ C(n,r) where r cannot be bigger than n
We can try our latest discovery for a 12 units long wall;
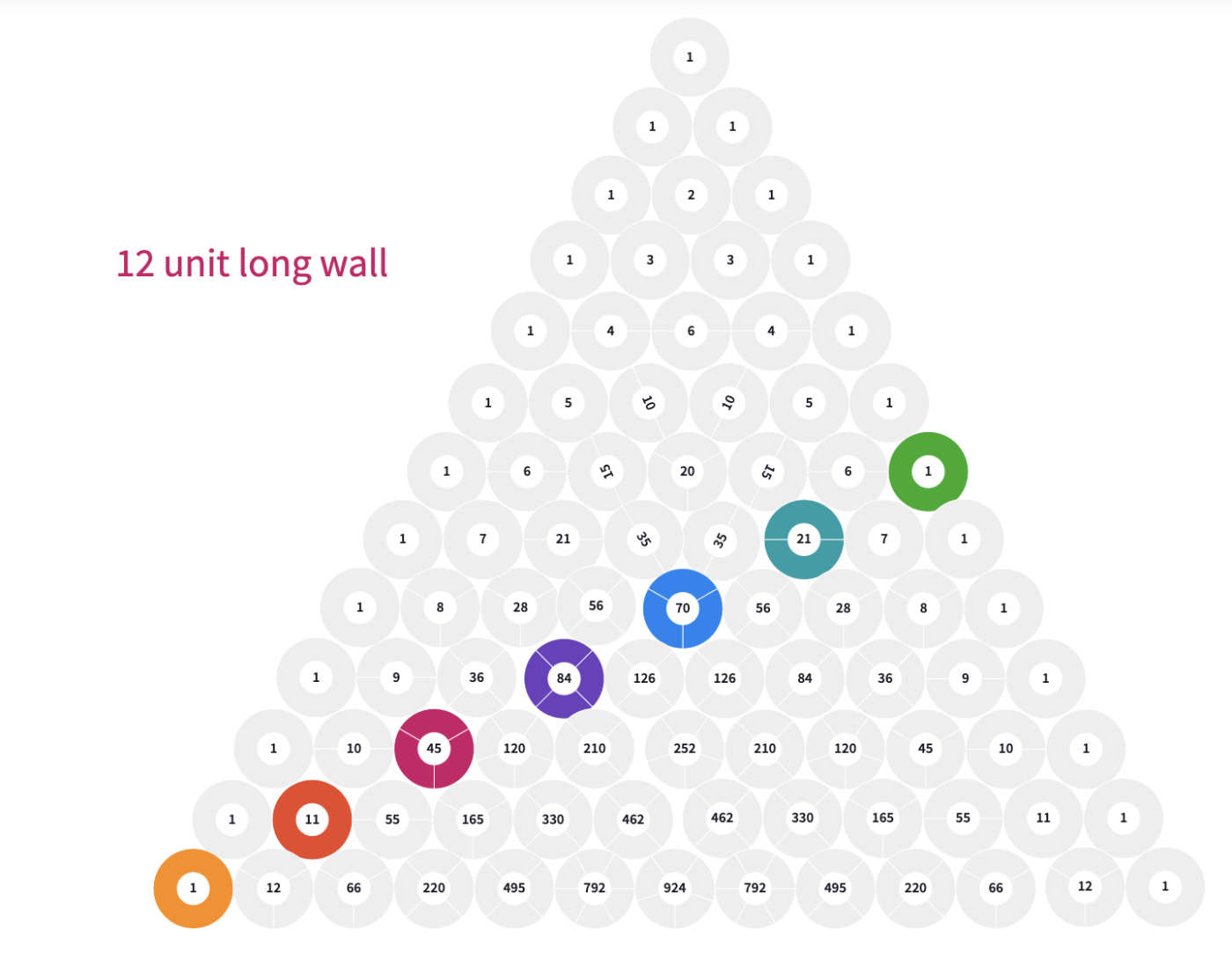
With Fibonacci sequence; 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233
With the Combination method;
C(12,0) + C(11,1) + C(10,2) + C(9,3) + C(8,4) + C(7,5) + C(6,6) >>
1 + 11 + 45 + 84 + 70 + 21 + 1 = 233