Overview and Objective
In this lesson, students explore the five Platonic Solids and their properties while also proving geometrically that there cannot be a sixth platonic solid.
Warm-Up
Consider having students work on the warm-up in groups. Ask them to Insert the Platonic Solids from the 3D collection of Polypad to a blank canvas to explore their properties closely. Ask them to record what they notice and what they wonder about the Platonic Solids.
Then, collect groups' findings to reach a general definition of Platonic Solids. You may want to use concept map canvas to organize their findings visually.
Some of the students' responses might be
- All of them are 3D Convex Polyhedra.
- They are made up of only one type of polygon.
- The faces are regular polygons.
- They have the same number of faces meeting at every vertex.
You may also want to involve the rich history of Platonic Solids in the discussion.
Platonic Solids were first mentioned by Plato around 350 BC. He believed that all matter in the universe consists of four elements: Air, Earth, Water, and Fire. He thought that every element corresponds to one of the Platonic solids, while the fifth one would represent the universe as a whole. Also, the famous German astronomer Johannes Kepler used platonic solids to describe the orbits of planets and the Sun.
Here is an example concept map of Platonic Solids

Main Activity
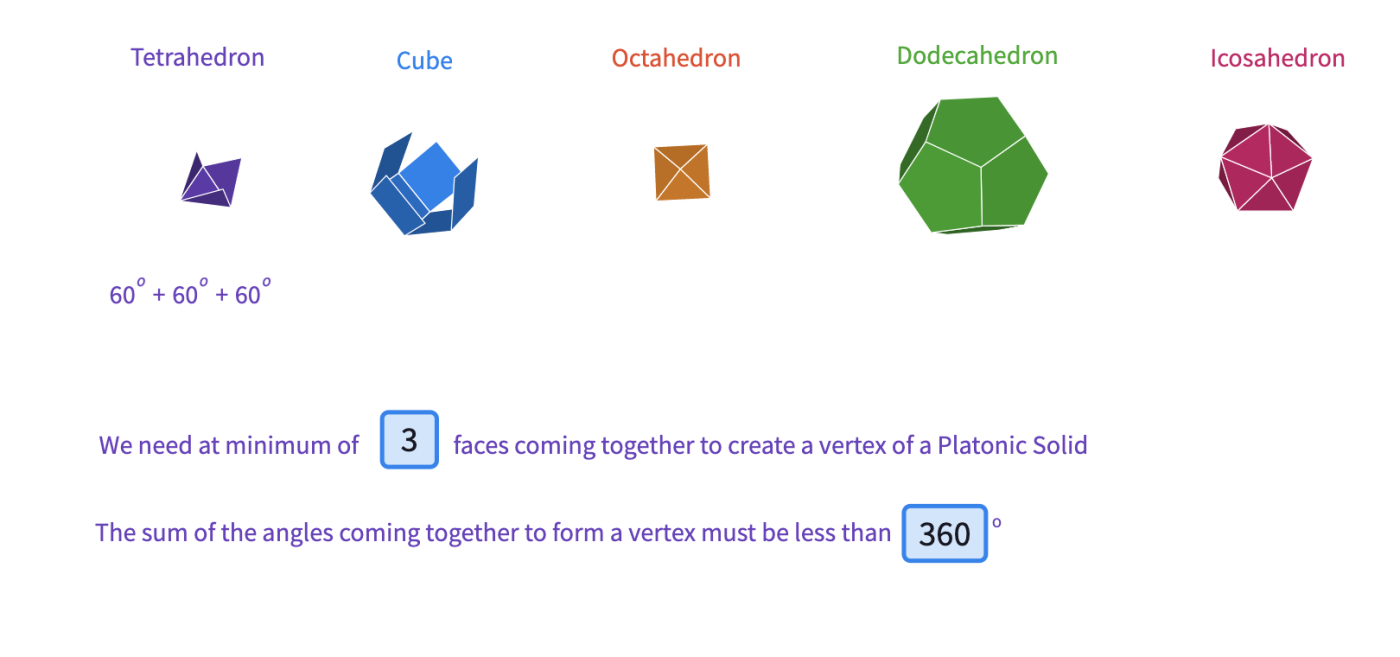
Platonic Solids are regular Polyhedra whose faces are all the same kind of regular polygon, and the same number of faces meet at every vertex. There are five known platonic solids. Discuss the shape and the number of faces for each.
- Tetrahedron - made up of 4 equilateral triangles
- Cube - made up of 6 squares
- Octahedron - made up of 8 equilateral triangles
- Icosahedron - made up of 20 equilateral triangles
- Dodecahedron - made up of 12 regular pentagons.
Share Mathigon's Tweet below and ask them to investigate if it is possible to have another platonic solid. You may notice the date of the Tweet, but don't yet mention that to students.

Share this canvas with students and discuss the following:
- At least how many faces need to come together to form a vertex of a 3D solid?
- Find the angles at each vertex for each Platonic solid. What is the sum of the angles at each vertex can maximum be?
Remind students that they can unfold the solids to answer these questions.
Clarify with the students that these two statements are the biggest clues for their investigation.
Allow students time to work on assembling regular polygons starting from the smallest regular polygon: equilateral triangles;

Let them assemble different numbers of triangles next to each other and find if the sum of the angles is less than . They then explore if they create a vertex by checking with the folding the net option. Students will continue to assemble different regular polygons in different numbers. They can create a table on the canvas to organize their findings.

Closure
Invite students to share their work by clarifying these results;
- When equilateral triangles come together to create a vertex, the sum of angles is . In this way, we get the shape .

- When equilateral triangles come together to create a vertex, the sum of angles is . In this way, we get the shape .

- When equilateral triangles meet at every vertex, the sum of angles is . In this way, we get the shape .

- When equilateral triangles meet at every vertex, the sum of angles is . So, we simply get a tessellation. We can conclude that when 5 triangles meet at a vertex, that exhausts the possibilities of triangles and therefore we can move on to consider squares.

- When squares meet at every vertex, the sum of angles is . In this way, we get the shape .

- When squares meet at every vertex, the sum of angles is , so we get another tessellation. Next, try regular pentagons.

- When pentagons meet at every vertex, the sum of angles is . In this way, we get the shape . pentagons will create an angle bigger than so that dodecahedron is the only platonic solid formed by pentagons.

- The next regular polygons to try are hexagons. If hexagons meet at every vertex, the sum of angles is , and we immediately get a tessellation. since there is no space for more than three, it seems like there are no Platonic solids consisting of hexagons.

The same also happens for all regular polygons with more than six sides. They don’t tessellate, and we certainly don’t get any three-dimensional polygons. In this way, we proved that there are only five platonic solids.
At the end of the lesson, show students the tweet again by highlighting the date this time. It is no more than a mathematical joke!
Support and Extension
For students ready for additional extension in this lesson, consider asking about the duals of platonic solids. We can turn a polyhedron into its dual by “replacing” every face with a vertex and every vertex with a face. Let them explore the surprising fact about the duals of each platonic solid.

For students needing additional support with these ideas, you can share the table format of the proof to organize their findings easier.
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.