Overview
Visual patterns are a powerful tool to engage students in deep mathematical thought and exploration. The tools on Polypad can help make students' thinking visible to classmates and teachers.
Using Visual Patterns in Class
- Share one of the Polypad canvasses below with students. Click here to learn how to share canvasses with students and for an overview of how students can share their completed work with teachers.
- Invite students to create the next three pictures in the pattern. Copying tiles is important in these tasks. This video provides an overview of three ways to copy tiles in Polypad.
- The auto-correcting answer boxes for figures 4, 5, and 6 provide immediate feedback to students about whether or not they continued the pattern correctly. Once they've done so, students can predict the number of objects in a larger figure number and then create an algebraic expression to represent the nth figure in the pattern.
- The ability to easily change colors, add tiles, move tiles, and rotate tiles within Polypad can help students make their thinking visible to classmates. The video below shows one way in which the Polypad tools helps to make student thinking visible.
- Some of the patterns below are 3D forms on a 2D space. Using the isometric background can help:
Visual Pattern Canvasses
Below are some visual patterns. Upon opening one in Polypad, select "Save Copy" in the Library panel to save a copy to your account. Click here to learn how to make your own visual patterns using the Question Builder feature in Polypad.
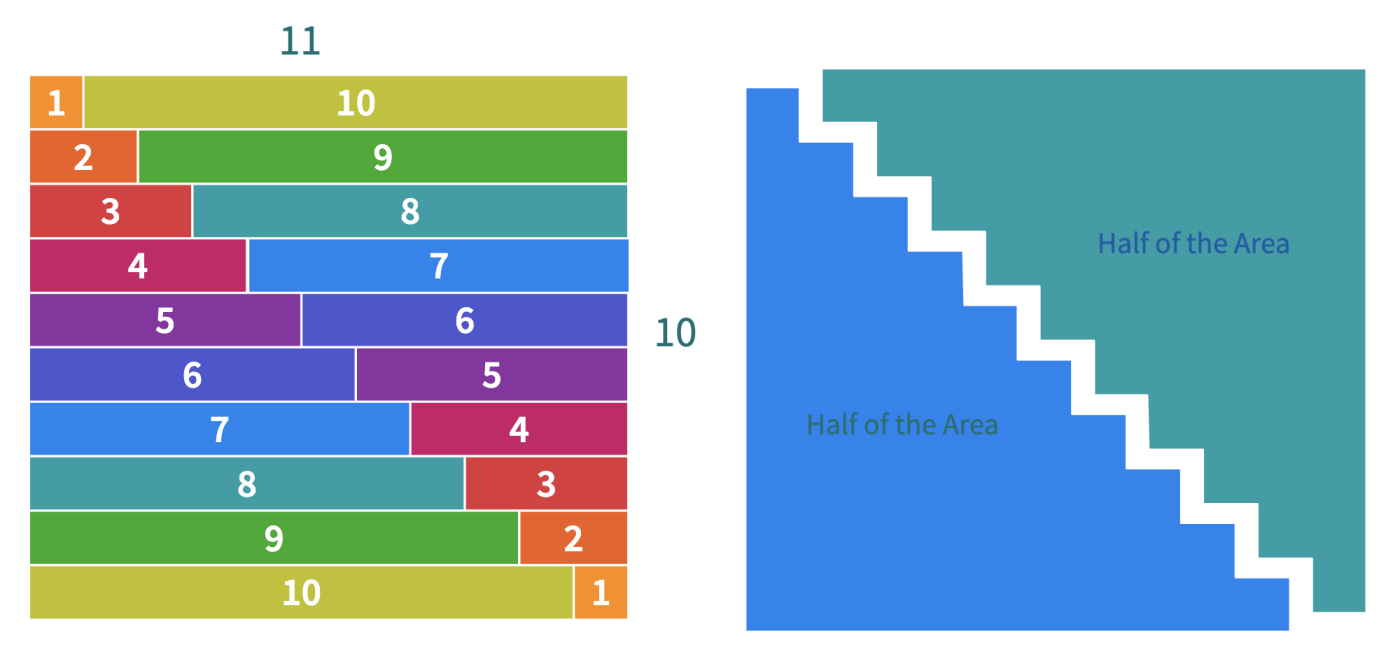
The number of rhombuses increases by one in each step. One way to express the algebraic expression for the nth term of the sequence of triangles is .
One way to express the algebraic expression for the nth term of this sequence is .
This pattern show the Triangular Numbers. Each number of objects can be arranged into a triangle. One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this pattern is
One way to express the algebraic expression for the nth term of this sequence is . Below are some different ways to view this pattern.
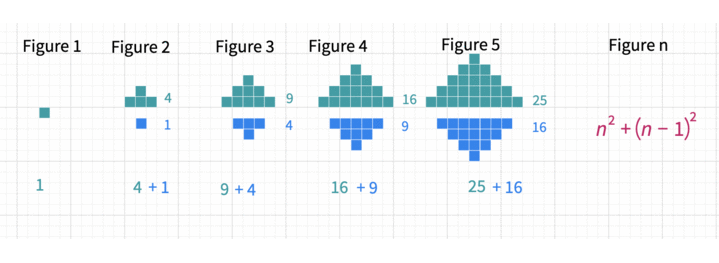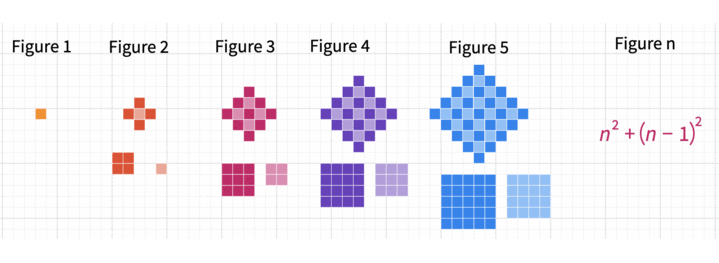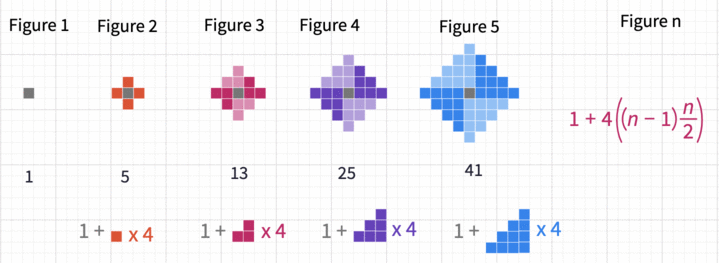
This pattern is a different visual representation of the square numbers.
One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this sequence is The nth term can also be expressed as .
One way to express the algebraic expression for the nth term of this sequence is
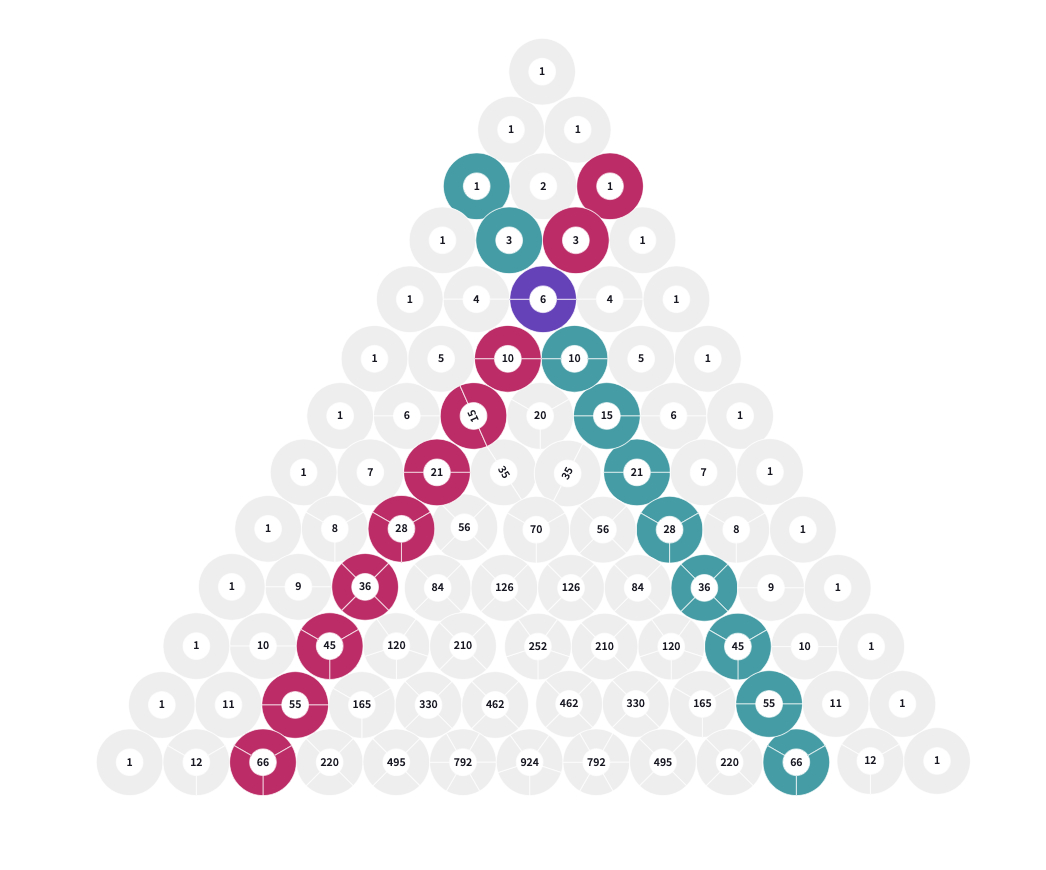
This pattern shows the Tetrahedral Numbers. A tetrahedral number can be represented as a pyramid with a triangular base and three sides called a tetrahedron.
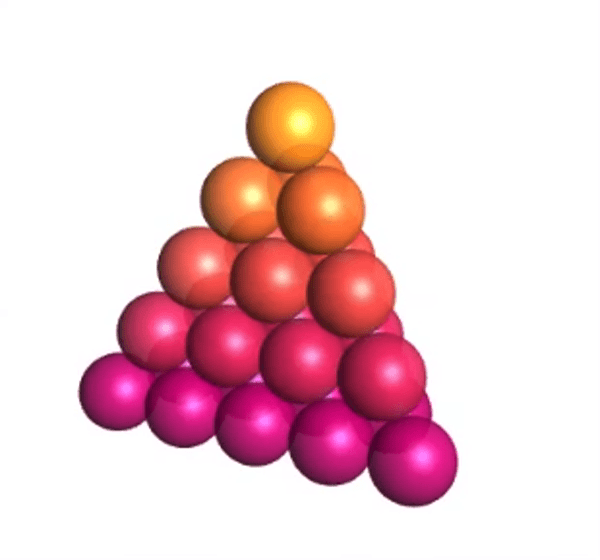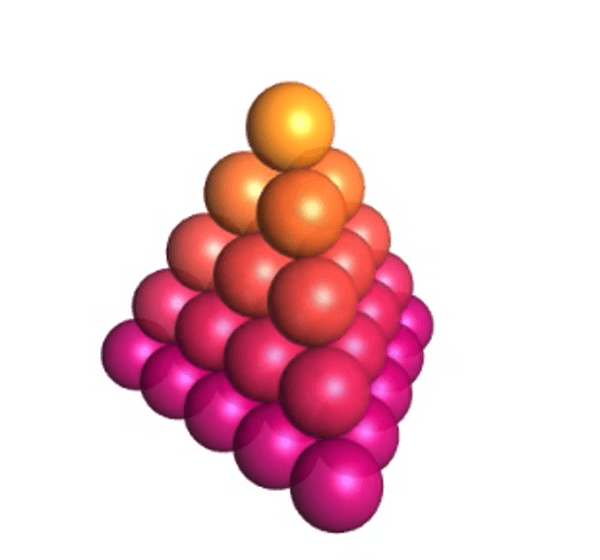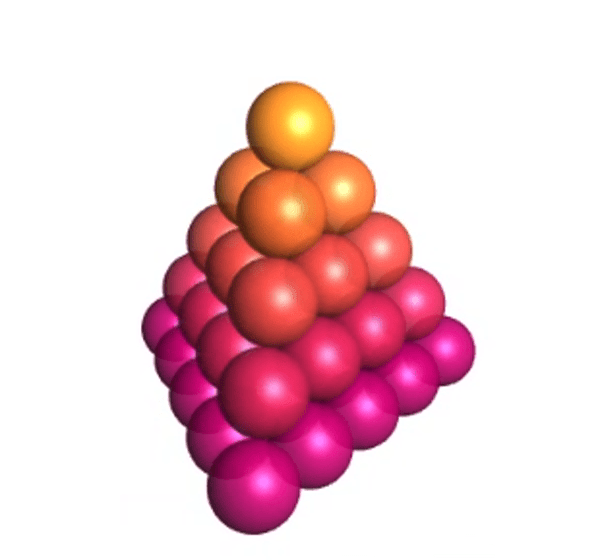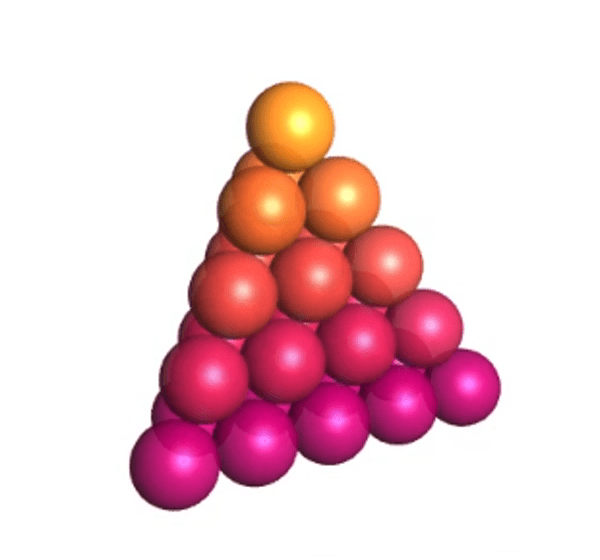
Each tetrahedral number is the sum of the triangular numbers. The image above shows 15 spheres on the bottom layer, 10 spheres in the lighter pink layer, 6 in the red layer, 3 in the orange layer, and finally 1 sphere on top. 1, 3, 6, 10, 15 are triangular numbers. 1 + 3 + 6 + 10 + 15 = 35, creating the 5th tetrahedral number.
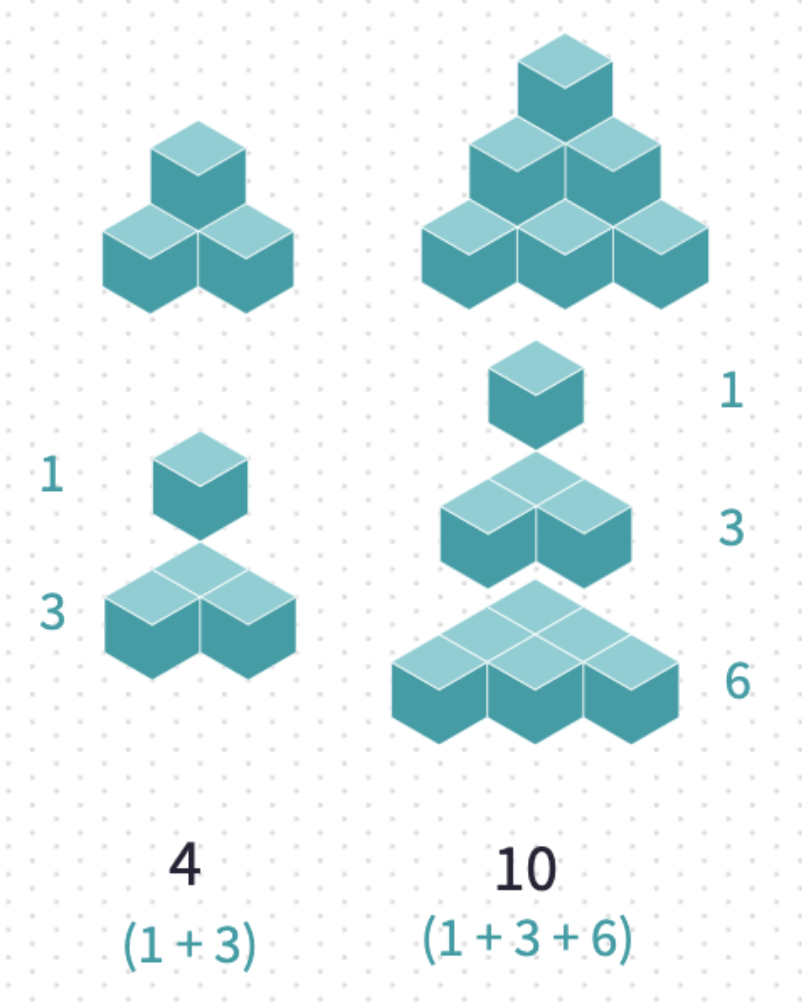
One way to express the algebraic expression for the nth term of this sequence is :
The is the pattern of cube numbers and can can be expressed as :
One way to express the algebraic expression for the nth term of this sequence is .
This pattern is sometimes called the pool or border pattern. The blue tiles represent the pool tiles whereas the red tiles are the border tiles. The number of border tiles for an "n by n" square can be expressed in many different ways.
One way to express the algebraic expression for the nth term of this sequence is
The ratio between the consecutive terms is constant and is equal to 3. One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this sequence is .
One way to express the algebraic expression for the nth term of this sequence is
One way to express the algebraic expression for the nth term of this sequence is
The light green triangles can be expressed as . The sequence of the to dark green triangles can be expressed as . So, one way to express the total number of triangles for the nth term is or .
One way to express the algebraic expression for the nth term of this sequence is .
Credits
Some of the patterns on this page come from visualpatterns.org, created by Fawn Nguyen, and licensed under a Creative Commons Attribution 4.0 International License.
Have a visual pattern you've created you'd like added to this list? Email the Polypad link to teachers@mathigon.org.