Lesson Outline
This task uses the Polypad number tiles to help students develop a better understanding of remainders when dividing. The model of remainders as squares left over in an array can be used to create simple proofs of ideas such as “Two odd numbers always add together to make an even number” or “If you add together two multiples of four, the answer will also be a multiple of four”. This structural approach for thinking about numbers and remainders can be a powerful foundation for thinking about algebraic representations of patterns and sequences.
Warm Up
The purpose of the warm-up is to introduce the idea of changing the number of columns in an array in Polypad, and identifying the remainder as the number of squares left over. To do this, create the number 24 in number tiles and then merge the tiles.
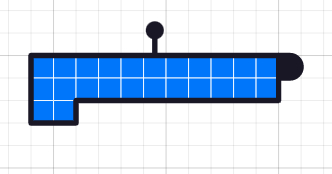
Now invite students to predict what will happen as you drag the black handle on the right of the shape to the left, decreasing the number of columns. As you reveal each step, take time to discuss what the diagram is showing us:
After shrinking the column width by one, we have two rows of 9 and an incomplete row of 6. 24 divided by 9 is 2 remainder 6.
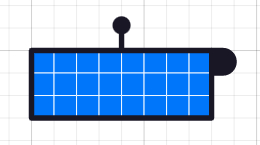
After shrinking the column width again, we have three rows of 8, and no incomplete rows. 24 divided by 8 is 3.
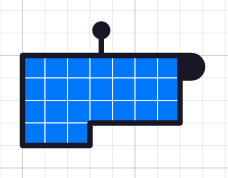
After shrinking the column width once more, we have three rows of 7 and an incomplete row of 3. 24 divided by 7 is 3 remainder 3.
If you think your class may need extra scaffolding of this idea before moving to the main activity, consider making this Polypad with students. You could either create the whole Polypad as a class or start it together and then have students finish on their own. You could save the canvas that you’ve started and then share it with students.
Main Activity
Show students this Polypad canvas. Note - Polypad automatically centers all tiles on the canvas. So, before sharing the canvas with students in class, make sure the top of the shapes are hidden by the top of the screen as shown in the screenshot below. Show students that only parts of the figures are shown by slightly dragging each figure down the screen to reveal a little more of the shape. Be carful not to reveal the whole figure. Click here for a quick video example.

Students will now work on trying to find the total number of tiles. For students with their own device, invite them to use Polypad to try to create a figure that can fit into all the arrangements above. Make sure students know how to merge, split, and copy tile arrangements.
Simple guessing and checking is a fine initial approach. As students move to a more structured approach, some may need guidance. One way to approach this problem systematically is for students to explore numbers of their own in Polypad and find out what connects the numbers that create each picture, rather than focusing on a number that can create all of them. Creating ones like the first picture tells us the number must be odd, the second tells us it is two more than (or one less than) a multiple of three, and so on.
Consider how you want students to share their solution with you. One options would be for students to create a Polypad with all the images and the division and remainders shown. See this Polypad for an example.
Once students think they have found the answer, they can explore these follow-up questions:
- Can you find a number (bigger than 1) that has a remainder of 1 when you divide it by 2, 3, 4, 5 and 6? Can you find more than one?
- Can you find a number that has a remainder of 1 when you divide it by 2, 2 when you divide it by 3, 3 when you divide it by 4, and 4 when you divide it by 5?
- Can you find a number that has a remainder of 1 when you divide it by 3, 3 when you divide it by 5, and 5 when you divide it by 7?
- Invite students to make their own example of this type of question. If they have access to a device, they can create their question on a Polypad like the one shown at the start of the Main Activiy.
Towards the end of the lesson, invite students to share the strategies they used to work out the hidden number, and reveal it by pulling down the shapes on the Polypad canvas. Take some time to discuss why we need the extra clue that the number is less than 60; since 2, 3, 4, 5 and 6 are all factors of 60, once we have the solution of 35 we could add 60 to it to get another solution. If appropriate, you could introduce some algebra to represent the solution set – the hidden number could be of the form 60n-25 for n=1, 2, 3… (or 60n+35 for n=0, 1, 2…).
Possible Solutions to Follow-Up Questions
Question 1: 61 works. It is odd, and has a remainder of 1 when divided by 3, 4, 5 and 6 as shown here:

Since 60 is a multiple of 2, 3, 4, 5 and 6, adding 60 will not change the remainder, so 121, 181, 241 and so on will also work, in fact any number in the sequence 60n+1.
Question 2: Another way to think about this is that the number is 1 less than a multiple of 2, 3, 4 and 5, so 59 is a solution.
Question 3: This time we’re looking for something that is 2 less than a multiple of 3, 5 and 7, so 103 is the first number that fits.
Support and Extension
To ease students into this activity, you could start by inviting them to explore just two different remainders: Can you find a number which has a remainder of 1 when you divide by 2, and 4 when you divide by 7? Can you find another?
The image shows that once students have found the example of 11 which is four more than a multiple of 7, and also an odd number, they can make a rectangle of 14, so it can be added onto the 11 they have already found to create additional answers.
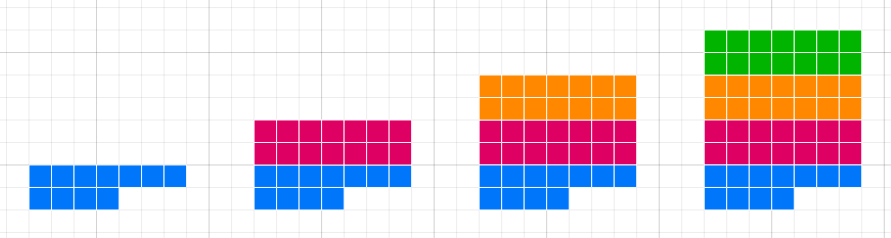
One extension idea is for students to continue to explore the ideas hinted at in the follow-up questions. They could create challenges of their own, and perhaps investigate impossible challenges. For example, it is impossible to find a number that has a remainder of 3 when you divide by 15 and a remainder of 2 when you divide by 9. Students might explore this by writing out the two relevant sequences: 3, 18, 33, 48, … and 2, 11, 20, 29, 38, 47… They may observe that as the sequences don’t coincide before both are greater than 45 (the lowest common multiple of 9 and 15), they will never coincide. Alternatively, they may notice that the first sequence is always a multiple of 3, and the second sequence is always two more than a multiple of 3.
The Remainders Game on NRICH is a fantastic activity to continue practicing the topics in this lesson.