Puzzle Board
The Lune of Hippocrates is said to be one of the first mathematical calculations of an area between curved lines.
Hints
As in the other problems, different approaches can be used to solve this problem.
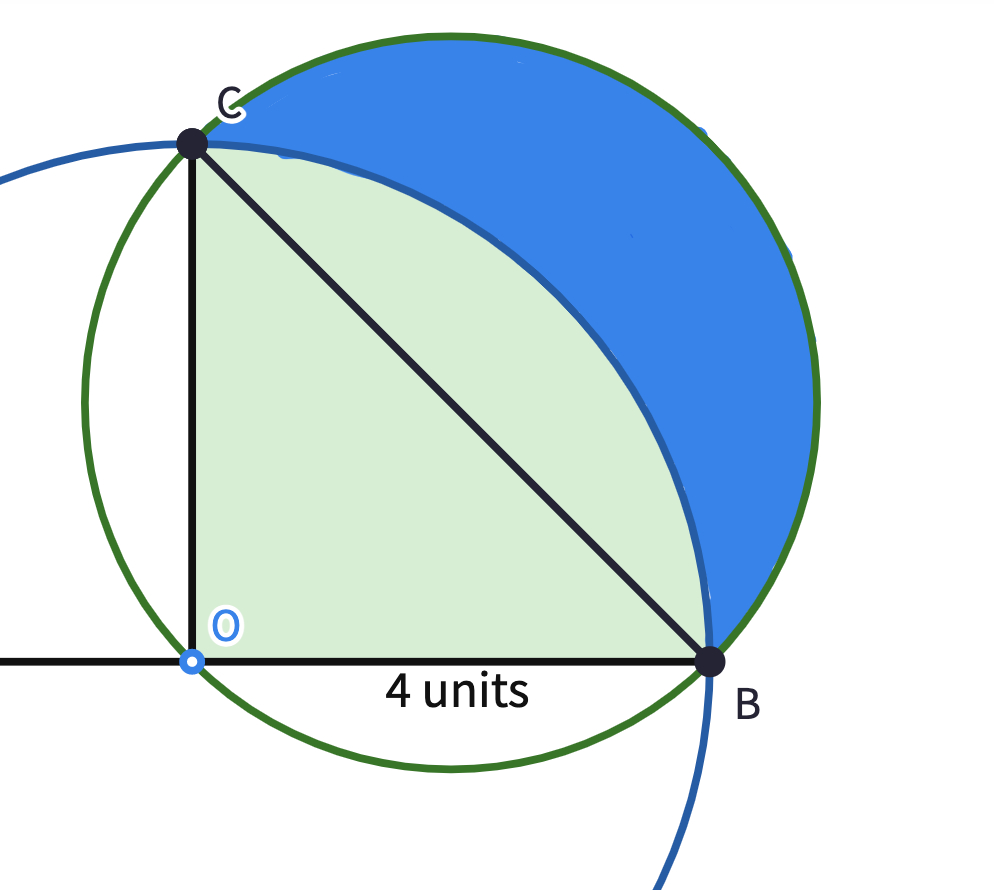
- Focus on the properties of the BOC Triangle. What kind of triangle is BOC?
- What is the length of OC?
- What is the area of the triangle BOC?
- Focus on the properties of the green region. What is its area?
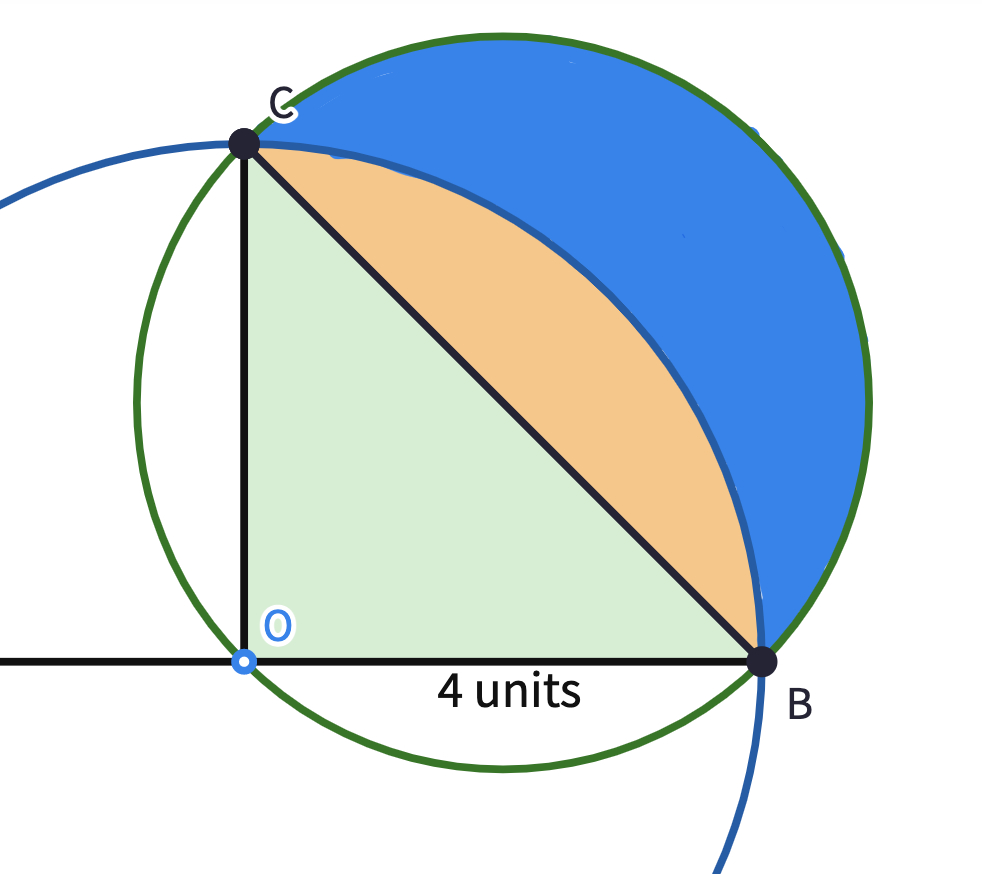
- Is it possible to find the area of the yellow region?
- After determining the area of the yellow region can you calculate the area of the lune?
Solution
While the circle’s area formula was not even known at that time, Hippocrates of Chios (400 BCE) managed to square the lune area. Squaring means constructing a square with the same area of the given shape.
The area of the lune is equal to the area of the indicated isosceles right triangle in the given diagram.
More on the Lunes of Hippocrates
Later, Arab mathematician Alhazen (c. 965 – 1040) calculated the area of the two lunes that are formed on the two sides of a right triangle. The lunes formed in this way are known as the lunes of Alhazen. Determine the relationship between the area of these lines and the right triangle.
In the 19th century, two more squarable lunes were found by T. Clausen and in the 20th century, it is proven that there are only five squarable lunes.
Next
If you like this puzzle, try Rhind Papyrus Problem